


Next: 5. Prefix Gröbner Bases
Up: Solving One-Sided Equations in
Previous: 3. The General Case
4. Conclusions
So far we have derived a generating set of solutions for a system of inhomogeneous
equations using prefix Gröbner bases.
Now in many monoid or group rings, e.g. when the respective structure is commutative,
such prefix Gröbner bases cannot be expected to be finite in general.
On the other hand there are examples where finite Gröbner bases exist for finitely generated
one or even two-sided ideals in monoid or group rings with respect to reduction relations other
than prefix reduction.
In general monoid and group rings (one and two-sided) Gröbner bases can be characterized
in terms of two kinds of test sets
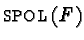 corresponding to critical polynomials of the generating set
corresponding to critical polynomials of the generating set 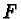 called s-, g-, or m-polynomials depending on the context,
called s-, g-, or m-polynomials depending on the context,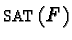 corresponding to critical polynomial multiples of the generating set
corresponding to critical polynomial multiples of the generating set 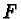 (compare
the saturation techniques described e.g. in [5]).
(compare
the saturation techniques described e.g. in [5]).
Both sets are dependent on the reduction relation chosen for the monoid or group ring.
Now for those cases where a set 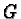 is a Gröbner basis
and these two test sets
is a Gröbner basis
and these two test sets 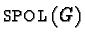 and
and 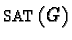 are finite, a finite set of solutions
for the homogeneous equation
are finite, a finite set of solutions
for the homogeneous equation
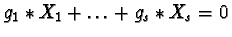 where
where
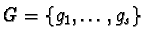 can be derived as described in Section 2.
Examples where these ideas are applicable since the test sets are finite and finite respective
one-sided Gröbner bases exist are free and plain group rings.
Even two-sided finite Gröbner bases and finite test sets exist for commutative monoid rings
and polycyclic group rings.
A similar extension can be done to treat systems of inhomogeneous equations as described in
Section 3.
The details are subject of an extended version of this paper.
can be derived as described in Section 2.
Examples where these ideas are applicable since the test sets are finite and finite respective
one-sided Gröbner bases exist are free and plain group rings.
Even two-sided finite Gröbner bases and finite test sets exist for commutative monoid rings
and polycyclic group rings.
A similar extension can be done to treat systems of inhomogeneous equations as described in
Section 3.
The details are subject of an extended version of this paper.



Next: 5. Prefix Gröbner Bases
Up: Solving One-Sided Equations in
Previous: 3. The General Case
| ZCA Home |
Reports |