


Next: Computational Aspects
Up: Effective Construction of Algebraic
Previous: Symbolic Hamburger-Noether expressions
This section is devoted to the ``core'' of the presented algorithm,
the Brill-Noether residue theorem. In an intuitive
formulation it states that ``the intersection divisors of 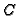 with all adjoint curves of a fixed degree
with all adjoint curves of a fixed degree 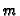 form a complete linear system,
up to being shifted by the adjoint divisor''.
form a complete linear system,
up to being shifted by the adjoint divisor''.
Let 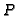 be a closed point of
be a closed point of 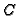 . We introduce the local (resp. semilocal) rings
. We introduce the local (resp. semilocal) rings
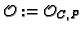 , resp.
, resp.
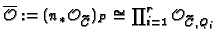 , where
, where
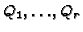 denote the closed places of
denote the closed places of 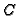 over
over 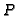 . Note that
. Note that
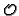 is a subring
of
is a subring
of
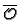 . The conductor
. The conductor
is an ideal both in
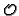 and in
and in
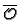 .
It defines a divisor
.
It defines a divisor
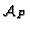 on
on
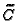 whose support is
whose support is
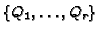 , the set of all places of
, the set of all places of 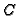 over the
singular point
over the
singular point 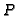 . Recall that such a place corresponds to a unique
branch of
. Recall that such a place corresponds to a unique
branch of 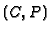 . By abuse of notation, we sometimes do not distinguish
between the place and the corresponding branch.
. By abuse of notation, we sometimes do not distinguish
between the place and the corresponding branch.
Definition 2.4
We call the divisor
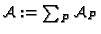
the
adjunction
divisor (or the
divisor of double points)
of
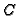
. Its support is the set of all places
over singular points of
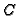
.
Remark 2.5
The adjunction divisor
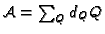
is rational, that is,
conjugate branches
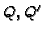
satisfy
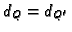
.
We have
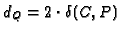
if
is a place over
an
irreducible plane curve singularity
, resp.
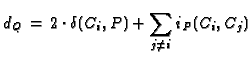 |
(2) |
if
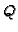
corresponds to the local branch
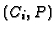
of
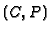
(
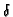
denoting the
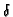
-invariant and
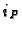
the local intersection multiplicity at
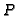
).
Alternatively, one can use the
Dedekind formula to compute the
multiplicities
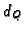
: let
![$ \varphi_Q:\mathbf{F}[[x,y]]\to \overline{\mathbf{F}}[[t]]$](img384.gif)
be a
primitive parametrization of the branch
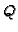
then
if the respective expressions are finite (notice that either
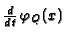
or
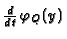
does not vanish identically).
Notation.
Let
![$ H\in \mathbf{F}[X,Y,Z]_m$](img388.gif) be a homogeneous form of degree
be a homogeneous form of degree
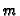 such that
such that 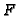 does not divide
does not divide 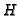 .
Then we denote by
.
Then we denote by 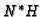 the intersection divisor on
the intersection divisor on
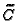 cut out by the (preimage under
cut out by the (preimage under 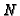 of the) plane
curve defined by
of the) plane
curve defined by 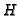 .
.
Note that 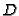 is an adjoint divisor iff the intersection multiplicity
of
is an adjoint divisor iff the intersection multiplicity
of 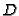 with every local branch
with every local branch 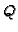 of
of 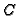 is at least
is at least 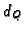 .
.
Proposition 2.7 (Brill-Noether residue theorem)
Let
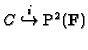
be a
reduced absolutely irreducible plane projective curve
given by the homogeneous polynomial
![$ F\in \mathbf{F}[X,Y,Z]_d$](img294.gif)
. Moreover, let
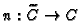
be the
normalization and
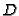
a rational divisor on
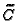
.
Finally, let
![$ H_0\in \mathbf{F}[X,Y,Z]_m$](img398.gif) be an adjoint form of degree
be an adjoint form of degree
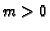 such that
such that
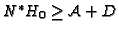 . Then we can identify
. Then we can identify
under the isomorphism
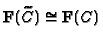
induced by
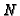
.
This proposition is an immediate corollary
of
Theorem 2.8 (M. Noether)
Let
![$ G,H\in \mathbf{F}[X,Y,Z]$](img403.gif)
be
homogeneous forms such that
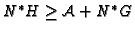
. Then
there exist homogeneous forms
![$ A,B\in \mathbf{F}[X,Y,Z]$](img405.gif)
such that
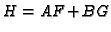
.
For a complete proof we refer to [42], pp. 215ff,
resp. [28], Prop. 4.1.
Remark 2.9
Haché [
18] has shown that a
form
![$ H_0\in \mathbf{F}[X,Y,Z]_m$](img398.gif)
as in the Brill-Noether
residue theorem exists whenever
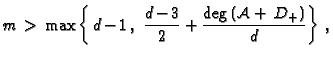 |
(3) |
where
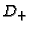
denotes the effective part of the divisor
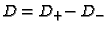
.



Next: Computational Aspects
Up: Effective Construction of Algebraic
Previous: Symbolic Hamburger-Noether expressions
Christoph Lossen
2001-03-21
![]() with all adjoint curves of a fixed degree
with all adjoint curves of a fixed degree ![]() form a complete linear system,
up to being shifted by the adjoint divisor''.
form a complete linear system,
up to being shifted by the adjoint divisor''.
![]() be a closed point of
be a closed point of ![]() . We introduce the local (resp. semilocal) rings
. We introduce the local (resp. semilocal) rings
![]() , resp.
, resp.
![]() , where
, where
![]() denote the closed places of
denote the closed places of ![]() over
over ![]() . Note that
. Note that
![]() is a subring
of
is a subring
of
![]() . The conductor
. The conductor
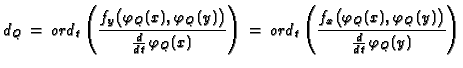
![]() ,
,
![]() ,
such that
,
such that
![]() .
Then we call
.
Then we call ![]() an adjoint form and the plane curve defined
by
an adjoint form and the plane curve defined
by ![]() an adjoint curve of
an adjoint curve of ![]() .
.
 be a
reduced absolutely irreducible plane projective curve
given by the homogeneous polynomial
be a
reduced absolutely irreducible plane projective curve
given by the homogeneous polynomial
![]() be an adjoint form of degree
be an adjoint form of degree
![]() such that
such that
![]() . Then we can identify
. Then we can identify
![$\displaystyle \mathcal{L}(D)\,\equiv\, \left\{ \left[\frac{H}{H_0}\right] \in \...
...H,\\
N^{\ast}H\geq N^{\ast}H_0\!-D
\end{array}\right\} \cup \bigl\{0 \bigr\} $](img401.gif)