


Next: Preliminaries, Notations
Up: Three Algorithms in Algebraic
Previous: Integral closure of an
Effective Construction of Algebraic Geometry Codes
Goppa's construction of linear codes using algebraic geometry, the
so-called geometric Goppa or AG codes, was a
major breakthrough in the history of coding theory. In particular, it
was the first (and only) construction leading to a
family of codes with parameters above the Gilbert-Varshamov bound
[41].
There exist several (essentially equivalent) ways to construct AG codes
starting from a smooth projective curve
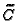 defined over
a finite field
defined over
a finite field
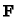 . Mainly, we should like to mention the L-,
resp. the
. Mainly, we should like to mention the L-,
resp. the 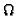 -construction.
-construction.
Given rational points
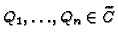 and a rational divisor
and a rational divisor 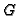 on
on
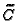 having disjoint support with the divisor
having disjoint support with the divisor
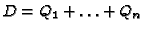 ,
the AG code
,
the AG code
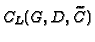 , resp.
, resp.
 , is the image of the
, is the image of the
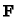 -linear map
-linear map
In practice, there are two main difficulties when looking for an
effective method to compute the
generator matrices of such codes: Given a plane (singular) model 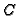 of
of
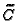 , how to compute the places of
, how to compute the places of 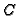 and how to compute
a basis for the linear system
and how to compute
a basis for the linear system
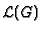 (cf. below),
resp. for the vector space of rational
one-forms
One possible solution, making use of blowing-up theory (to compute
the places of
(cf. below),
resp. for the vector space of rational
one-forms
One possible solution, making use of blowing-up theory (to compute
the places of 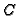 ) and of the (classical) Brill-Noether algorithm (for
the computation of a basis of
) and of the (classical) Brill-Noether algorithm (for
the computation of a basis of
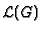 ) is presented in
[28,19]. In the following, we should like to
point to the modified approach of Campillo and Farrán [3],
using Hamburger-Noether expansions instead of blowing-up theory, and
to present in some detail the resulting algorithm as
implemented in the computer algebra system SINGULAR [17].
) is presented in
[28,19]. In the following, we should like to
point to the modified approach of Campillo and Farrán [3],
using Hamburger-Noether expansions instead of blowing-up theory, and
to present in some detail the resulting algorithm as
implemented in the computer algebra system SINGULAR [17].
Subsections



Next: Preliminaries, Notations
Up: Three Algorithms in Algebraic
Previous: Integral closure of an
Christoph Lossen
2001-03-21
![]() defined over
a finite field
defined over
a finite field
![]() . Mainly, we should like to mention the L-,
resp. the
. Mainly, we should like to mention the L-,
resp. the ![]() -construction.
-construction.
![]() and a rational divisor
and a rational divisor ![]() on
on
![]() having disjoint support with the divisor
having disjoint support with the divisor
![]() ,
the AG code
,
the AG code
![]() , resp.
, resp.
![]() , is the image of the
, is the image of the
![]() -linear map
-linear map