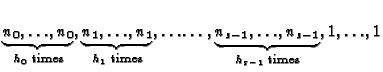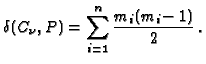We recall the definition of Hamburger-Noether
expansions (HNE), resp. symbolic Hamburger-Noether
expressions, for the branches of a reduced plane curve singularity.
They can be regarded as the analogue of Puiseux expansions when working
over a field of positive characteristic (cf. the discussion in
[2], 2.1). As being the case for Puiseux expansions, many
invariants of plane curve singularities (such as the multiplicity
sequence, the ![]() -invariant, the intersection multiplicities of
the branches, etc.), can be computed directly from the corresponding
system of HNE.
-invariant, the intersection multiplicities of
the branches, etc.), can be computed directly from the corresponding
system of HNE.
Let ![]() be a point and
be a point and ![]() local parameters at
local parameters at
![]() . Moreover, let the germ
. Moreover, let the germ ![]() be given by a local equation
be given by a local equation
![]() with irreducible decomposition
with irreducible decomposition
![]() . Finally,
let's suppose that
. Finally,
let's suppose that ![]() is a transversal parameter for
is a transversal parameter for
![]() , that is, the order of
, that is, the order of ![]() is equal to the order of
is equal to the order of
![]() .
.
If the local equation of ![]() is polynomial in
is polynomial in ![]() , i.e.,
, i.e.,
![]() , then the last (infinite) row of (1) can
be replaced, equivalently, by a (finite) implicit equation
, then the last (infinite) row of (1) can
be replaced, equivalently, by a (finite) implicit equation
![$\displaystyle g(z_s,z_{s-1})\,=\,0\,,\qquad g\in \mathbf{F}_{\text{ext}}[x,y]\,, \quad
\frac{\partial g}{\partial z_{s-1}} (0,0) \neq 0\,.$](img349.gif)
Any HNE leads to a primitive
parametrization
![]() of the
branch (setting
of the
branch (setting ![]() and mapping
and mapping
![]() ,
,
![]() ). It can be computed from a sHNE up to
an arbitrary finite degree in
). It can be computed from a sHNE up to
an arbitrary finite degree in ![]() .
.
To perform the algorithm one does not need any knowledge
about the irreducible factorization of ![]() in
in
![]() . Moreover, in the reducible case, the probably
necessary (finite) field extension is not performed a priori, but
by successive (primitive) extensions introduced exactly when needed
for computations (factorization).
. Moreover, in the reducible case, the probably
necessary (finite) field extension is not performed a priori, but
by successive (primitive) extensions introduced exactly when needed
for computations (factorization).