Computing the divisors $N^\ast H$

The intersection divisors $N^\ast H$ can be computed by the following algorithm:

Input

$F\in \mathbf{F}[X,Y,Z]_d$, $L$ list of closed places $[Q]$ of $C$ (defined by $F=0$), $H\in \mathbf{F}[X,Y,Z]_m$.

Output

Extended list of closed places $[Q]$ and list of integers $m_{[Q]}$ such that $N^\ast H=\sum_{[Q]} m_{[Q]}[Q]$.

1. Affine Intersection. Let $h(x,y):=H(x,y,1)$, $f(x,y):=F(x,y,1)$ and consider $I:=\langle h,f\rangle$. Proceed as in Step 1 of the algorithm in Section 2.4.1 to obtain a set of (triangular) ideals corresponding to the set of closed points in $V(I)$. For each closed point $[P]$ in $V(I)$ do the following:
   • check for each closed place $[Q]$ in $L$ whether $[Q]$ lies above $[P]$ (that is, the first entry of the triple representing $[Q]$ has to be $[P]$). If this is the case, compute the multiplicity $m_{[Q]}=ord_t h\bigl(\varphi_Q(x),\varphi_Q(y)\bigr)$, where $\varphi_Q$ is the primitive parametrization obtained from the sHNE (third entry) of $[Q]$.
   • If there is no such $[Q]$ in $L$ then compute the sHNE for the (smooth) germ $(C,P)$, add the resulting place $[Q]$ to the list $L$ and proceed as before to obtain $m_{[Q]}$.
2. Intersection at infinity. Let 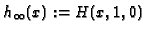$h_{\infty}(x):=H(x,1,0)$ and compute a prime factorization of the polynomial $h_{\infty}\in \mathbf{F}[x]$,
   $$\hspace*{1.2cm} h_\infty=h_{\infty,1}\cdot \ldots \cdot h_{\infty,d''}\in \mathbf{F}[x]\,, \qquad d''\!\leq d\,.$$
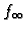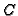   Each factor that appeared also in the prime factorization (4) of $f_{\infty}$ corresponds to a closed point $\big[(a_j\!:\!\!\:1\!\!\::\!\!\:0)\big]$ in the intersection of $C$ with the plane curve defined by 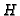$H$. For the corresponding closed places $[Q]$ we compute
   $$m_{[Q]}= ord_t H\bigl(\varphi_Q(x)\!\!\:+\!\!\:a_j,\,1,\, \varphi_Q(z)\bigr)\,,$$
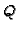   where $\varphi_Q:\mathbf{F}[[x,z]]\to \overline{\mathbf{F}}[[t]]$ is the primitive parametrization obtained from the sHNE of $Q$ (cf. Step 4 of the algorithm in Section 2.4.1).

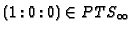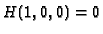   Finally, if $(1\!\!\::\!\!\:0\!\!\::\!\!\:0)\in PTS_{\infty}$ and $H(1,0,0)=0$ then we compute for the corresponding closed places $[Q]$ the multiplicities

   $$m_{[Q]} =ord_t H\bigl(1,\varphi_Q(y),\varphi_Q(z)\bigr)\,.$$