


Next: Computing a basis for
Up: Computational Aspects
Previous: Computing the divisors
Computing
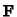 -bases of adjoint forms
-bases of adjoint forms
Let
Monom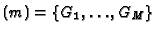 denote the
monomial
denote the
monomial
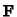 -basis for
-basis for
![$ \mathbf{F}[X,Y,Z]_m$](img503.gif) , resp. the corresponding
vector of monomials. We represent a homogeneous
form
, resp. the corresponding
vector of monomials. We represent a homogeneous
form
![$ H\in \mathbf{F}[X,Y,Z]_m$](img388.gif) by the vector
by the vector
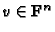 such that
such that
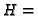 Monom
Monom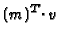 . To compute
. To compute
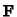 -bases of adjoint forms as needed by the Brill-Noether algorithm,
we apply the following algorithm:
-bases of adjoint forms as needed by the Brill-Noether algorithm,
we apply the following algorithm:
- Input
-
![$ F\in \mathbf{F}[X,Y,Z]_d$](img294.gif) ,
,
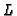 list of closed places of
list of closed places of 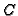 (defined by
(defined by 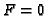 ),
),
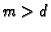 a positive integer,
a positive integer,
non-negative integers ![$ d_{[Q]}$](img508.gif) ,
, ![$ [Q]\in L$](img509.gif) , s.th.
, s.th.
![$ \mathcal{A}=\sum_{[Q]} d_{[Q]}[Q]$](img510.gif) ,
,
non-negative integers ![$ n_{[Q]}$](img511.gif) ,
, ![$ [Q]\in L$](img509.gif) , s.th.
, s.th.
![$ E=\sum_{[Q]} n_{[Q]}[Q]$](img512.gif) .
.
- Output
-
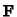 -basis of a subspace of
complementary to
-basis of a subspace of
complementary to
![$ W:=F\cdot \mathbf{F}[X,Y,Z]_{m-d}$](img514.gif) (given in form of a matrix of coefficients w.r.t.
Monom
(given in form of a matrix of coefficients w.r.t.
Monom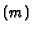 ).
).
- The subspace
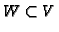 of forms divisible by
of forms divisible by
 . Compute the matrix
. Compute the matrix
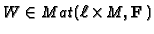 with
with
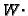 Monom
Monom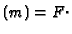 Monom
Monom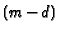 .
.
Note that
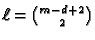 ,
,
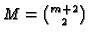 .
.
- The space
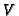 .
For each closed place
.
For each closed place ![$ [Q]$](img484.gif) with
with
![$ m_{[Q]}:=d_{[Q]}+n_{[Q]}>0$](img524.gif) do the following:
Finally, concatenate the
do the following:
Finally, concatenate the ![$ A_{[Q]}$](img531.gif) to obtain
to obtain
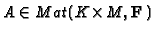 with
with
![$ K=\sum_{[Q]}
k_Qm_{[Q]}$](img533.gif) and compute
and compute 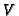 as the kernel of
as the kernel of 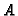 , that is
, that is
- Compute a complement of
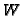 in
in 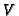 . This can be done, for
instance, by using the lift command in SINGULAR.
. This can be done, for
instance, by using the lift command in SINGULAR.



Next: Computing a basis for
Up: Computational Aspects
Previous: Computing the divisors
Christoph Lossen
2001-03-21
![]() ,
,
![]() .
.
![$\displaystyle G_j\bigl(\varphi_Q(x),\varphi_Q(y)\bigr) = \sum_{i=0}^{m_{[Q]}-1}
a_{ij}t^i\,, \quad j=1,\dots, M\,,$](img526.gif)
![$\displaystyle \left( \begin{array}{c}
A_Q\\
A_Q^{(1)}\\
\vdots\\
A_Q^{(k_Q-1)}
\end{array}\right) \in Mat(\!\:k_Qm_{[Q]}\!\times\!\!\: M,\mathbf{F}\,)\,.
$](img530.gif)