


Next: Example
Up: Computational Aspects
Previous: Computing -bases of adjoint
Let 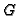 be any
rational divisor on
be any
rational divisor on
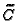 . The algorithms of the
preceding sections finally allow to compute an
. The algorithms of the
preceding sections finally allow to compute an
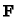 -basis of
-basis of
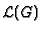 by the Brill-Noether Algorithm (cf. Prop. 2.7):
by the Brill-Noether Algorithm (cf. Prop. 2.7):
- Input
-
![$ F\in \mathbf{F}[X,Y,Z]_d$](img294.gif) ,
,
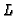 list of closed places of
list of closed places of
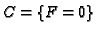 ,
,
non-negative integers ![$ d_{[Q]}$](img508.gif) ,
, ![$ [Q]\in L$](img509.gif) , s.th.
, s.th.
![$ \mathcal{A}=\sum_{[Q]} d_{[Q]}[Q]$](img510.gif) ,
,
integers ![$ g_{[Q]}$](img537.gif) ,
, ![$ [Q]\in L$](img509.gif) , s.th.
, s.th.
![$ G=\sum_{[Q]} g_{[Q]}[Q]$](img538.gif) .
.
- Output
- Vector space basis of
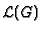 (in terms of rational
functions on
(in terms of rational
functions on 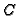 ).
).
- Choose
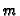 sufficiently large (for instance, according to
(3), above).
sufficiently large (for instance, according to
(3), above).
- Compute
![$ H_0\in \mathbf{F}[X,Y,Z]_m$](img398.gif) ,
,
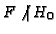 , such that
, such that
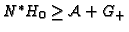 . To do so, we compute an
. To do so, we compute an
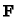 -basis for a vector
subspace of
complementary to
-basis for a vector
subspace of
complementary to
![$ W:=F\cdot \mathbf{F}[X,Y,Z]_{m-d}$](img514.gif) (cf. Section 2.4.4) and choose any element
(cf. Section 2.4.4) and choose any element 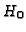 of this
basis (for instance, with the minimal number of monomials).
of this
basis (for instance, with the minimal number of monomials).
- Compute the effective divisor
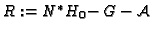 (cf. Section 2.4.3).
(cf. Section 2.4.3).
- Compute an
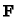 -basis
-basis
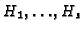 of a vector subspace of
complementary to
of a vector subspace of
complementary to
![$ W=F\cdot \mathbf{F}[X,Y,Z]_{m-d}$](img546.gif) (cf. Section 2.4.4).
(cf. Section 2.4.4).
- Return the set of rational functions
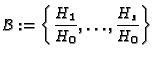 .
.



Next: Example
Up: Computational Aspects
Previous: Computing -bases of adjoint
Christoph Lossen
2001-03-21
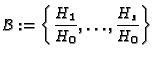 .
.