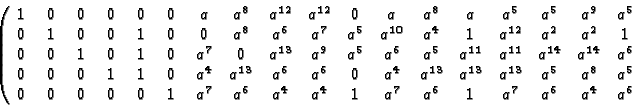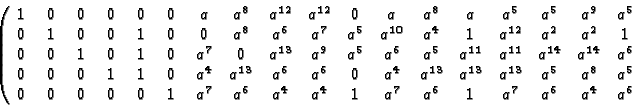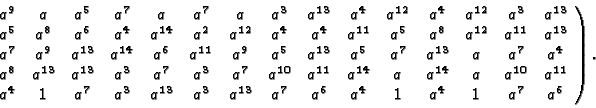Next: V-filtration and spectral numbers
Up: Effective Construction of Algebraic
Previous: Computing a basis for
The above algorithms are implemented in the
library brnoeth.lib of SINGULAR, together with procedures
for coding and decoding and are distributed with version 2.0. To
compute an example, we first have to load the library.
LIB "brnoeth.lib";
Let 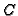 be the absolutely irreducible plane projective curve given
by the affine equation
be the absolutely irreducible plane projective curve given
by the affine equation
![$ y^2+y+x^5\in \mathbf{F}_2[x,y]$](img548.gif) . We compute
all places up to degree
. We compute
all places up to degree 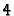 , by
, by
ring r=2,(x,y),dp;
poly f=y2+y+x5;
list CURVE=Adj_div(f);
==> The genus of the curve is 2.
CURVE=NSplaces(3,CURVE); // places up to degree 4=1+3
We can consider the curve as being defined over
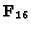 in
order to get many rational places.
in
order to get many rational places.
CURVE=extcurve(4,CURVE);
==> Total number of rational places : NrRatPl = 33
The degree of the computed (conjugacy classes of) places is
displayed by
list L=CURVE[3]; L;
==> [1]: 1,1 [2]: 1,2 [3]: 1,3
==> [4]: 2,1
==> [5]: 3,1 [6]: 3,2
==> [7]: 4,1 [8]: 4,2 [9]: 4,3 [10]: 4,4
==> [11]: 4,5 [12]: 4,6 [13]: 4,7
In particular, besides the
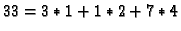 rational places
over
rational places
over
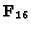 there are
there are 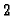 closed places
closed places
![$ [Q_5],[Q_6]$](img553.gif) of
degree
of
degree 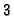 . The adjunction divisor is given by
. The adjunction divisor is given by  , where
, where
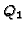 is the unique (rational) point on
is the unique (rational) point on
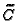 mapping to the singular point
mapping to the singular point
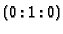 . This can be read off
as follows:
. This can be read off
as follows:
CURVE[4]; // the mult's d_Q at L[1],L[2],...
// (zeroes omitted)
==> 8
def r1=CURVE[5][1][1];
setring r1;
POINTS[1]; // coordinates of the base point of L[1]
==> [1]: 0 [2]: 1 [3]: 0
PARAMETRIZATIONS[1]; // parametrization of L[1]
==> [1]: _[1]=t3+t8
_[2]=t5+t15
// exact up to order:
[2]: 8,10
We construct the evaluating AG-code
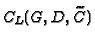 where
all rational points of
where
all rational points of
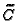 appear in the support of
appear in the support of 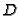 and
and
![$ G=[Q_5]+[Q_6]$](img558.gif) .
.
intvec G=0,0,0,0,1,1,0,0,0,0,0,0,0;
intvec D=1..33;
def R=CURVE[1][4];
setring R;
matrix CODE=AGcode_L(G,D,CURVE);
The echelon form of the resulting
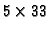 -matrix is
Note that the constructed code
-matrix is
Note that the constructed code
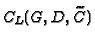 has block
length 33, dimension 5 and designed distance
has block
length 33, dimension 5 and designed distance
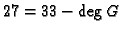 .
On the other hand, the first row corresponds to a word of weight 27,
whence the designed distance coincides with the minimal distance.
As a result, we get that
.
On the other hand, the first row corresponds to a word of weight 27,
whence the designed distance coincides with the minimal distance.
As a result, we get that
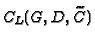 is a
is a
![$ [33,5,27]$](img563.gif) -code. Note that
the parameters, that is, the information rate
-code. Note that
the parameters, that is, the information rate 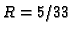 and the relative minimum distance
and the relative minimum distance
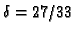 , lie
above the Gilbert-Varshamov bound.
, lie
above the Gilbert-Varshamov bound.



Next: V-filtration and spectral numbers
Up: Effective Construction of Algebraic
Previous: Computing a basis for
Christoph Lossen
2001-03-21