


Next: 6. Reduction in Polycyclic
Up: Introducing Reduction to Polycyclic
Previous: 4. On the Relations
5. Reduction in Nilpotent Group Rings
Let  be a nilpotent group given by a convergent PCNI-presentation as
described in section 2.
The next example illustrates that no total, well-founded admissible
ordering can exist for a non-trivial group due to the
existence of inverses.
be a nilpotent group given by a convergent PCNI-presentation as
described in section 2.
The next example illustrates that no total, well-founded admissible
ordering can exist for a non-trivial group due to the
existence of inverses.
Example 5
Let
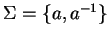
and
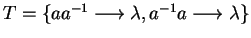
be a presentation of a group

.
Let

denote the rational numbers.
Suppose we simply require divisibility of the head term to allow reduction.
Then we could reduce the
polynomial
![$a^2 + 1 \in {\bf Q}[{\cal G}]$](img558.gif)
at the monomial
a2 by the polynomial
a-1 +
a as

.
This would give
and the polynomial
-
a4 + 1 likewise would be reducible by
a-1 +
a at the monomial -
a4 causing an
infinite reduction sequence.
Hence we will give additional restrictions on the divisibility
property required to allow reduction in order to prevent that a monomial
is replaced by something larger.
Since  in general is not commutative, we will at first restrict ourselves
to right multiples to define reduction.
How reduction using left multiples can be done is outlined in section
6 for the more general case that
in general is not commutative, we will at first restrict ourselves
to right multiples to define reduction.
How reduction using left multiples can be done is outlined in section
6 for the more general case that  is given as a
convergent PCP-presentation.
is given as a
convergent PCP-presentation.
Definition 9
Let
p,
f be two non-zero polynomials in
![${\bf K}[{\cal G}]$](img5.gif)
.
We say that
f quasi-commutatively (qc-) reduces p to
q at
a monomial
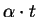
of
p in one step, denoted by

,
if
- (a)
-
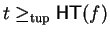 ,
and
,
and
- (b)
-
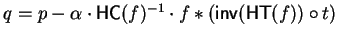 .
.
Quasi-commutative reduction by a set
![$F \subseteq {\bf K}[{\cal G}]$](img212.gif)
is denoted by
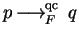
and abbreviates

for some
.
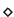
Notice that if f qc-reduces p at
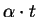 to q,
then t no longer is a term in q and by lemma 5, p > q holds.
This reduction is effective, as it is possible to decide, whether we have
to q,
then t no longer is a term in q and by lemma 5, p > q holds.
This reduction is effective, as it is possible to decide, whether we have
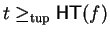 .
Further it is Noetherian and the translation lemma holds.
.
Further it is Noetherian and the translation lemma holds.
Lemma 9
Let F be a set of polynomials in
![${\bf K}[{\cal G}]$](img5.gif) and
and
![$p,q,h \in{\bf K}[{\cal G}]$](img567.gif) some
polynomials.
some
polynomials.
- 1.
- Let
 .
Then there are
.
Then there are
![$p',q' \in {\bf K}[{\cal G}]$](img569.gif) such that
such that
 and h=p'-q'.
and h=p'-q'.
- 2.
- Let 0 be a normal form of p-q with respect to
 .
Then there exists a polynomial
.
Then there exists a polynomial
![$g \in {\bf K}[{\cal G}]$](img572.gif) such that
such that
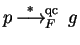 and
and
 .
.
Proof :
1.11.1
- 1.
- Let
 ,
where
,
where
 and
and
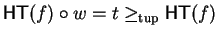 ,
i.e.
,
i.e.
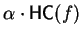 is the
coefficient of t in p-q.
We have to distinguish three cases:
is the
coefficient of t in p-q.
We have to distinguish three cases:
- (a)
-
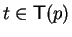 and
and
 :
Then we can eliminate the term t in the polynomials
p respectively q by qc-reduction. We then
get
:
Then we can eliminate the term t in the polynomials
p respectively q by qc-reduction. We then
get
 and
and
 ,
with
,
with
 ,
where
,
where
 and
and
 are
the coefficients of t in p respectively q.
are
the coefficients of t in p respectively q.
- (b)
-
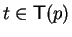 and
and
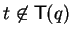 :
Then we can eliminate the term t in the polynomial
p by qc-reduction and get
:
Then we can eliminate the term t in the polynomial
p by qc-reduction and get
 and q = q'.
and q = q'.
- (c)
-
 and
and
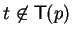 :
Then we can eliminate the term t in the polynomial
q by qc-reduction and get
:
Then we can eliminate the term t in the polynomial
q by qc-reduction and get
 and p = p'.
and p = p'.
In all cases we have
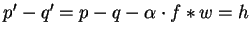 .
.
- 2.
- We show our claim by induction on k, where
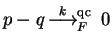 .
In the base case k=0 there is nothing to show.
Hence, let
.
In the base case k=0 there is nothing to show.
Hence, let
 .
Then by (1) there are polynomials
.
Then by (1) there are polynomials
![$p',q' \in {\bf K}[{\cal G}]$](img569.gif) such that
such that
 and h=p'-q'.
Now the induction hypothesis for
and h=p'-q'.
Now the induction hypothesis for
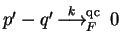 yields
the existence of a polynomial
yields
the existence of a polynomial
![$g \in {\bf K}[{\cal G}]$](img572.gif) such that
such that
 and
and
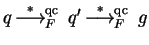 .
.
q.e.d.
1.11
In case  is a free Abelian group, qc-reduction coincides with Sims'
reduction for Laurent polynomials, as the condition
is a free Abelian group, qc-reduction coincides with Sims'
reduction for Laurent polynomials, as the condition
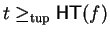 implies
that
implies
that
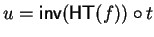 is aligned with
is aligned with
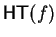 .
Notice that in the general nilpotent case u and
.
Notice that in the general nilpotent case u and
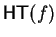 no longer need
to be aligned.
Furthermore the following example shows that even if they are aligned,
Sims' definition of reduction
cannot be carried over to nilpotent groups.
no longer need
to be aligned.
Furthermore the following example shows that even if they are aligned,
Sims' definition of reduction
cannot be carried over to nilpotent groups.
Example 6
Let
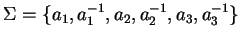
and

be
a convergent PCNI-presentation of the free nilpotent group on two
generators.
Then for
a1a2 and
a1a3 due to Sims' ordering we get

,
but for the aligned
elements
a1 and
a1a3 we find
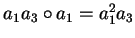
,
while

,
and hence
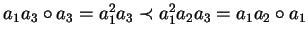
.
Gröbner bases as defined by Buchberger can now be specified for
right ideals in this setting as follows.
Definition 10
A set
![$G \subseteq {\bf K}[{\cal G}]$](img599.gif)
is said to be a
right Gröbner basis, if
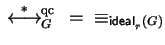
,
and

is confluent.
Since Buchberger's reduction always captures the ideal congruence, in order to
characterize Gröbner bases he only has to give a confluence criteria.
Now we find that in our setting we have to be more careful, as for
qc-reduction
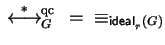 in general will
not hold.
One reason for this phenomenon is that a reduction step is not preserved under
right multiplication with elements of
in general will
not hold.
One reason for this phenomenon is that a reduction step is not preserved under
right multiplication with elements of  .
.
Example 7
Let
![${\bf Q}[{\cal G}]$](img602.gif)
be the group ring given in example
5.
Then for the polynomials
p =
a2 +
a and
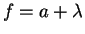
we find that
p is qc-reducible by
f.
This is no longer true for the multiple

.
Notice that, since
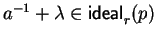
,
we have

,
but
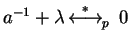
does not hold.
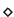
We will now introduce how we can extend the expressiveness of
qc-reduction.
We start by enabling the reducibility of special monomial multiples
of a polynomial by allowing to use not only the
polynomial itself but a special set of polynomial multiples for qc-reduction.
First let us take a look at what multiples are appropriate to later
on enable an effective characterization of a right Gröbner basis.
As our example shows, we have to pay attention to the problem that
different terms of a polynomial can
come to head position by right multiplication with group elements.
The next lemma states how right multiples which bring other terms to head position can be constructed in case they exist.
Lemma 10
Let p be a non-zero polynomial in
![${\bf K}[{\cal G}]$](img5.gif) .
In case there exists an element
.
In case there exists an element
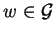 such that
such that
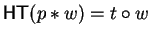 for some
for some
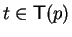 , let ad be the distinguishing
letter between t and
, let ad be the distinguishing
letter between t and
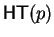 .
Then one can construct an
element
.
Then one can construct an
element
 such that
such that
 .
.
In particular, given p and
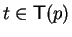 it is decidable whether there
exists an element
it is decidable whether there
exists an element
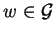 such that
such that
 .
.
Proof :
1.11.1
We show that for all polynomials
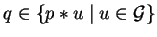 the
following holds:
In case
the
following holds:
In case
 for some
for some
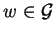 ,
,
 then one can construct an element
then one can construct an element
 where ad
is the distinguishing letter between ti and
where ad
is the distinguishing letter between ti and
 ,
and
,
and
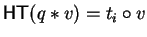 .
.
This will be done by induction on k where d = n-k.
In the base case let k=0, i.e., an is the
distinguishing letter between
 and
and
 .
Hence 1j = ij for all
.
Hence 1j = ij for all
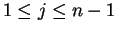 and
and
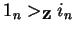 .
.
By our assumption there exists
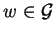 such that
such that
 ,
with
,
with
 ,
,
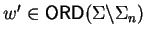 ,
and there exist
,
and there exist
 such that
such that
 and
and
 .
Thus
.
Thus
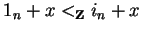 or, in case an is bounded by
or, in case an is bounded by
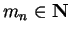 ,
,
 must hold.
First let us assume that the letter an is not bounded.
Then let us set
must hold.
First let us assume that the letter an is not bounded.
Then let us set
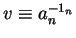 .
We show that for all
.
We show that for all
 we
have
we
have
 .
Note that for all tj with prefix
.
Note that for all tj with prefix
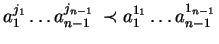 we have
we have
 ,
as
right multiplication with
,
as
right multiplication with
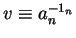 only changes the exponent of an in
the respective term.
It remains to look at those terms tj with
only changes the exponent of an in
the respective term.
It remains to look at those terms tj with
 .
Then we can apply lemma 3 as we have
.
Then we can apply lemma 3 as we have
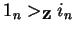 ,
,
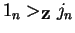 and as seen above there exists an element x such that
and as seen above there exists an element x such that
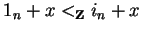 and
and
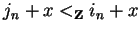 .
Therefore
.
Therefore
 and our claim must hold.
In case the letter an is bounded by mn, we set
and our claim must hold.
In case the letter an is bounded by mn, we set
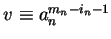 .
As before, for all tj which have a prefix
.
As before, for all tj which have a prefix
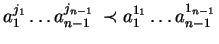 we have
we have
 .
Tor those tj with prefix
.
Tor those tj with prefix
 we know that the exponent of an in
we know that the exponent of an in
 cannot be mn -1 unless
tj = ti, and hence
cannot be mn -1 unless
tj = ti, and hence
 must hold.
must hold.
In the induction step let us assume that for all polynomials
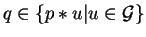 and
and
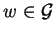 with
with
 ,
if the distinguishing letter ad
between
,
if the distinguishing letter ad
between
 and ti has index
and ti has index
 there exists
an element
there exists
an element
 such that
such that
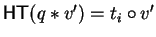 .
Now for
.
Now for
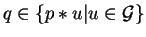 ,
,
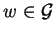 with
with
 let us assume that the distinguishing letter
between
let us assume that the distinguishing letter
between
 and ti has index d = n-k.
and ti has index d = n-k.
Since
 ,
for
,
for
 with
with
 ,
,
 ,
we know that there exist
,
we know that there exist
 and
and
 such that
such that
 and similarly
and similarly
 .
As
.
As
 then
then
 or,
in case an is bounded by
or,
in case an is bounded by
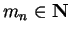 ,
,
 must hold.
In case ad is not bounded we can then set
must hold.
In case ad is not bounded we can then set
 .
We have to show that for all
.
We have to show that for all
 there exists
there exists
 such that we
have
such that we
have
 .
Note that for all tj with prefix
.
Note that for all tj with prefix
 we have
we have
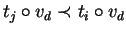 ,
as
right multiplication with
,
as
right multiplication with
 has no influence on the prefix
in
has no influence on the prefix
in
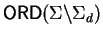 .
.
Therefore, it remains to look at those terms tj with
 and
and
 .
Since there further exists
.
Since there further exists
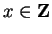 such that
such that
 and
and
 we can again apply lemma 3
to show our claim.
In case
we can again apply lemma 3
to show our claim.
In case
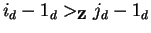 we are done.
Else we get id = jd and can apply the induction hypothesis since
the distinguishing letter between
we are done.
Else we get id = jd and can apply the induction hypothesis since
the distinguishing letter between
 and
and 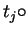 will be of
index greater than d, yielding an element
will be of
index greater than d, yielding an element
 and we can set
and we can set
 .
.
Now it remains to look at the case that ad is bounded by md.
Then we can set
 and proceed to construct
v as above.
and proceed to construct
v as above.
q.e.d.
1.11
Notice that the proof of this lemma shows that there is an algorithm
which computes some
 as desired in case it
exists and that the element w need not be known for this computation.
Hence we can enrich a polynomial by the set of those multiples which bring
other terms of the polynomial to head position.
But still there remain cases of multiples which are not qc-reducible
by this set of polynomials due to the fact that the ``divisibility''
criteria for the head term does not hold.
Just take a look at the polynomial p = a2+a in our example.
Then the head term of the multiple
as desired in case it
exists and that the element w need not be known for this computation.
Hence we can enrich a polynomial by the set of those multiples which bring
other terms of the polynomial to head position.
But still there remain cases of multiples which are not qc-reducible
by this set of polynomials due to the fact that the ``divisibility''
criteria for the head term does not hold.
Just take a look at the polynomial p = a2+a in our example.
Then the head term of the multiple
 results from the head
term a2 of p, but still
results from the head
term a2 of p, but still
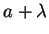 is not qc-reducible by p, since
a2 is no commutative prefix of a.
Therefore, let us consider some further special multiples.
For a polynomial p and a term
is not qc-reducible by p, since
a2 is no commutative prefix of a.
Therefore, let us consider some further special multiples.
For a polynomial p and a term
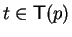 we call a term s
in a multiple
we call a term s
in a multiple  a t-term if
a t-term if
 .
The following lemma states that if in two right multiples of a polynomial
the head terms result from the same term t, then there is also a
right multiple of the polynomial with a t-term as head term which is in
some sense a common commutative prefix of the head terms of the
original two multiples.
In example 7 for
.
The following lemma states that if in two right multiples of a polynomial
the head terms result from the same term t, then there is also a
right multiple of the polynomial with a t-term as head term which is in
some sense a common commutative prefix of the head terms of the
original two multiples.
In example 7 for
 and
and
 ,
both head terms result from the same term a2 and
the head term a of
,
both head terms result from the same term a2 and
the head term a of
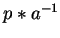 is a commutative prefix of the
head term a2 of
is a commutative prefix of the
head term a2 of
 .
.
Proof :
1.11.1
Let p, 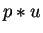 and
and 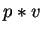 be as described in the lemma and
let the letters corresponding to our presentation be
be as described in the lemma and
let the letters corresponding to our presentation be
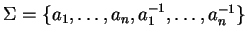 .
.
We show the existence of 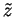 by constructing a sequence
by constructing a sequence
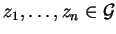 ,
such that for
,
such that for
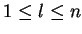 we have
we have
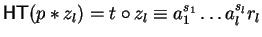 with
with
 and
and
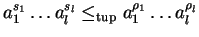 .
Then for
.
Then for
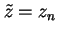 our claim holds.
our claim holds.
Let us start by constructing an element
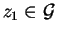 such that
such that
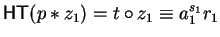 ,
,
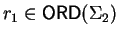 and
and
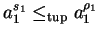 .
.
In case i1 = j1 or j1 =0 we can set z1 = v and
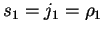 since
since
 .
Similarly in case i1 = 0 we can set z1 = u and
.
Similarly in case i1 = 0 we can set z1 = u and
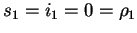 since
since
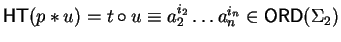 .
Hence let us assume
.
Hence let us assume
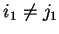 and both are non-zero.
and both are non-zero.
First suppose that
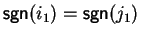 .
Notice that the construction in this case does not depend on whether a1 is bounded
or not.
Then if
.
Notice that the construction in this case does not depend on whether a1 is bounded
or not.
Then if
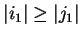 we again set z1 = v
since for
we again set z1 = v
since for
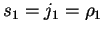 our claim holds.
In case
|j1| > |i1| we set z1 = u because for
our claim holds.
In case
|j1| > |i1| we set z1 = u because for
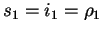 our claim holds.
our claim holds.
Now let us proceed with the case
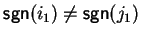 ,
i.e., a1 cannot be
bounded.
We construct
,
i.e., a1 cannot be
bounded.
We construct
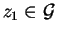 such that
such that
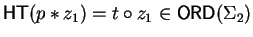 as
as
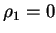 .
We claim that the letter a1 has the same exponent for all
terms in
.
We claim that the letter a1 has the same exponent for all
terms in
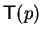 ,
say b.
In case this holds, no term in the polynomial
,
say b.
In case this holds, no term in the polynomial
 will
contain the letter a1 and the distinguishing letter between
will
contain the letter a1 and the distinguishing letter between
 and the term
and the term
 is at least of
index 2.
Furthermore we know
is at least of
index 2.
Furthermore we know
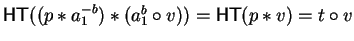 .
Thus by lemma 14 there exists an element
.
Thus by lemma 14 there exists an element
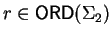 such that
such that
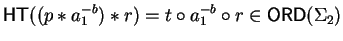 and thus we can set
z1 = a1-br and
and thus we can set
z1 = a1-br and
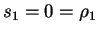 .
.
Hence it remains to prove our initial claim.
Suppose we have the representatives
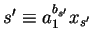 ,
,
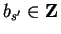 ,
,
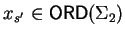 for the
terms
for the
terms
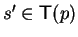 and
and
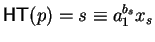 .
Then we know
.
Then we know
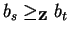 since
since
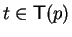 .
.
Hence in showing that the case
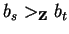 is not possible we
find that the exponents of a1 in s and t are equal.
To see this, let us study the possible cases.
If bs > 0 we have
is not possible we
find that the exponents of a1 in s and t are equal.
To see this, let us study the possible cases.
If bs > 0 we have
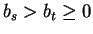 and hence there exists no
and hence there exists no
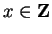 such that
such that
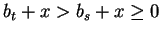 .
On the other hand bs < 0 either implies bt > 0 or
.
On the other hand bs < 0 either implies bt > 0 or
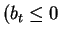 and
|bs| > |bt|).
In both cases there exists no
and
|bs| > |bt|).
In both cases there exists no
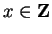 such that
bt + x < 0 and
|bt + x| > |bs + x|.
Hence bt = bs must hold as we know that t can be brought to
head position by u respectively v
such that the exponents of a1 in
such that
bt + x < 0 and
|bt + x| > |bs + x|.
Hence bt = bs must hold as we know that t can be brought to
head position by u respectively v
such that the exponents of a1 in
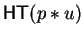 respectively
respectively
 have different
sign.
have different
sign.
It remains to show that there cannot exist a term
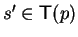 with
with
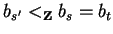 .
Let us assume such an s' exists.
Since
.
Let us assume such an s' exists.
Since
 and
and
 there
then must exist
there
then must exist
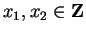 such that
such that
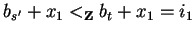 and
and
 .
Without loss of generality let us assume i1 > 0 and j1 < 0 (the
other case is symmetric).
In case bt < 0 we get that
bt + x1 = i1 > 0 implies
x1 > |bt| > 0.
Now, as
.
Without loss of generality let us assume i1 > 0 and j1 < 0 (the
other case is symmetric).
In case bt < 0 we get that
bt + x1 = i1 > 0 implies
x1 > |bt| > 0.
Now, as
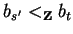 either implies
bs' > 0 or
either implies
bs' > 0 or
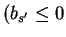 and
|bs'| < |bt|), we find
bs' + x1 > bt + x1 contradicting
and
|bs'| < |bt|), we find
bs' + x1 > bt + x1 contradicting
 .
On the other hand, in case bt > 0 we know
.
On the other hand, in case bt > 0 we know
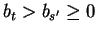 .
Furthermore,
bt + x2 = j1 < 0 implies x2 <0 and
|x2| >
bt.
Hence we get
bs' + x2 < 0 and
|bs' + x2| > |bt + x2|
contradicting
.
Furthermore,
bt + x2 = j1 < 0 implies x2 <0 and
|x2| >
bt.
Hence we get
bs' + x2 < 0 and
|bs' + x2| > |bt + x2|
contradicting
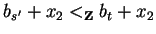 .
.
Thus let us assume that for the letter ak-1 we have
constructed
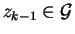 such that
such that
 with
with
 ,
,
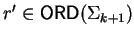 and
and
 .
We now show that we can find
.
We now show that we can find
 such that
such that
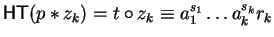 with
with
 and
and
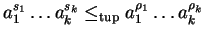 .
.
This will be done in two steps.
First we show that for the polynomials 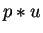 and
and
 with head terms
with head terms
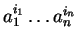 respectively
respectively
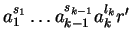 we can find an element
we can find an element
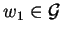 such that
such that
 ,
,
 and
and
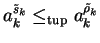 with
with
Then in case
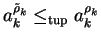 we are done
and set
we are done
and set
 and
and
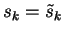 .
Else we can similarly proceed for the polynomials
.
Else we can similarly proceed for the polynomials 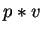 and
and
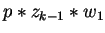 with head terms
with head terms
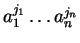 respectively
respectively
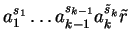 and find an element
and find an element
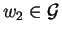 such that
for
such that
for
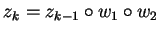 we have
we have
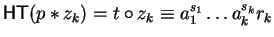 ,
,
 and
and
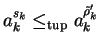 with
with
Then we can conclude
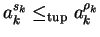 as in case sk = 0 we are immediately done and otherwise we get
as in case sk = 0 we are immediately done and otherwise we get
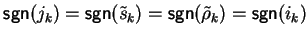 and
and
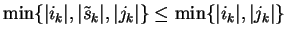 .
.
Let us hence show how to construct w1.
Remember that
 and
and
 for some
for some
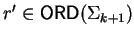 .
In case ik = lk or lk = 0 we can set
.
In case ik = lk or lk = 0 we can set
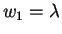 and
and
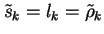 as
as
 .
Hence let
.
Hence let
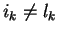 and
and
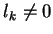 .
.
First let us assume that
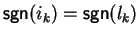 .
Then in case
.
Then in case
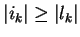 we are done by setting
we are done by setting
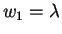 as again
as again
 will do with
will do with
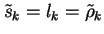 .
Therefore, let us assume that
|lk| > |ik|.
Without loss of generality let us assume that ak is not bounded12.
Then we consider the multiple
.
Therefore, let us assume that
|lk| > |ik|.
Without loss of generality let us assume that ak is not bounded12.
Then we consider the multiple
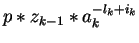 ,
i.e., the exponent of the letter ak in the term
,
i.e., the exponent of the letter ak in the term
 will be ik.
If
will be ik.
If
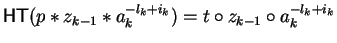 we are done because then
we are done because then
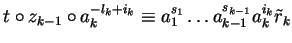 for some
for some
 and we can set
w1 = ak-lk+ik and
and we can set
w1 = ak-lk+ik and
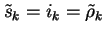 .
Otherwise we show that the t-term
.
Otherwise we show that the t-term
 in this multiple can be brought
to head position using an element
in this multiple can be brought
to head position using an element
 thus allowing
to set
thus allowing
to set
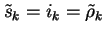 and
w1 = ak-lk+ikr as then we have
and
w1 = ak-lk+ikr as then we have
 where
where
 .
(Note that the product of two elements in
.
(Note that the product of two elements in
 is again an element in
is again an element in
 )
This follows immediately if we can prove that the exponent of ak in
the term
)
This follows immediately if we can prove that the exponent of ak in
the term
 is also ik.
Then we can apply lemma 14 to the polynomial
is also ik.
Then we can apply lemma 14 to the polynomial
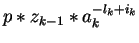 and the term
and the term
 .
Note that
.
Note that
 and
and
 have then distinguishing letter of at least index k+1 and
further
have then distinguishing letter of at least index k+1 and
further
 .
Therefore, we show that the exponent of ak in
the term
.
Therefore, we show that the exponent of ak in
the term
 is also ik.
Let
is also ik.
Let
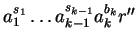 with
with
 be the term in
be the term in
 that became head
term (note that a candidate in
that became head
term (note that a candidate in
 for the head term in
for the head term in
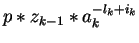 must have prefix
must have prefix
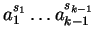 since
since
 and multiplication with
ak-lk +
ik only involves rk-1),
i.e.,
and multiplication with
ak-lk +
ik only involves rk-1),
i.e.,
 for some
for some
 and therefore
and therefore
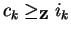 .
Then by lemma 4
there exist
.
Then by lemma 4
there exist
 and
and
 such that
such that
 for some
for some
 and
and
 ,
i.e.,
,
i.e.,
 for some
for some
 .
Note that the t-term is brought to head position by this
multiplication.
Now multiplying
.
Note that the t-term is brought to head position by this
multiplication.
Now multiplying
 by
z1z2 we find
by
z1z2 we find
 for some
for some
 .
This gives us
.
This gives us
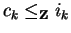 and thus
and thus
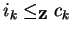 yields
ck = ik.
yields
ck = ik.
Finally, we have to check the case that
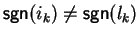 ,
i.e., ak is
not bounded in this case, and
,
i.e., ak is
not bounded in this case, and
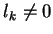 .
Let us take a look at the polynomial
.
Let us take a look at the polynomial
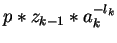 ,
i.e., the exponent of the letter ak in the term
,
i.e., the exponent of the letter ak in the term
 will be 0.
Suppose
will be 0.
Suppose
 ,
for some term
,
for some term
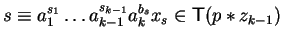 ,
,
 ,
i.e.,
ck = bs - lk.
In case this head term is already the corresponding t-term
,
i.e.,
ck = bs - lk.
In case this head term is already the corresponding t-term
 ,
we are
done and we set
w1 = ak-lk and
,
we are
done and we set
w1 = ak-lk and
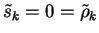 .
Now if we can show ck = 0,
by lemma 14 the t-term
.
Now if we can show ck = 0,
by lemma 14 the t-term
 can be
brought to head position using an element in
can be
brought to head position using an element in
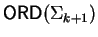 since
the distinguishing letter between
since
the distinguishing letter between
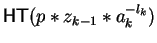 and the term
and the term
 then has at least index k+1 and we know
then has at least index k+1 and we know
 .
Hence, in showing that ck=0 we are done.
As before there exist
.
Hence, in showing that ck=0 we are done.
As before there exist
 and
and
 such that
such that
 for some
for some
 and
and
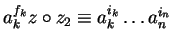 ,
i.e.,
,
i.e.,
 for some
for some
 .
Remember that this multiplication brings the t-term to head
position.
Hence multiplying
.
Remember that this multiplication brings the t-term to head
position.
Hence multiplying
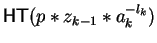 by z1z2
we find
by z1z2
we find
 for
some
for
some
 .
Thus we know
.
Thus we know
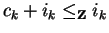 .
To see that this implies ck = 0 we have to distinguish three cases.
Remember that
ck = bs - lk and since our head term is an s-term
.
To see that this implies ck = 0 we have to distinguish three cases.
Remember that
ck = bs - lk and since our head term is an s-term
 for some
for some
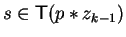 we know
we know
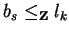 .
In case ik = 0, we have
.
In case ik = 0, we have
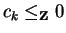 implying ck = 0.
In case ik > 0 then
implying ck = 0.
In case ik > 0 then
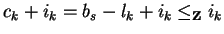 implies
implies
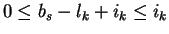 .
Furthermore, as lk < 0 we have
-lk + ik > ik implying bs < 0 and hence
.
Furthermore, as lk < 0 we have
-lk + ik > ik implying bs < 0 and hence
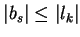 .
But then
.
But then
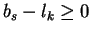 and
and
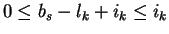 yields
ck = bs - lk = 0.
On the other hand, ik < 0 and lk > 0 imply
yields
ck = bs - lk = 0.
On the other hand, ik < 0 and lk > 0 imply
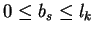 and hence
bs - lk + ik <0 yielding
and hence
bs - lk + ik <0 yielding
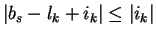 .
Since
.
Since
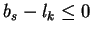 this inequation can only hold in case
ck = bs - lk = 0.
q.e.d.
this inequation can only hold in case
ck = bs - lk = 0.
q.e.d.
1.11
These two lemmata now state that given a polynomial, we can construct
additional polynomials, which are in fact right multiples of the
original polynomial, such that every right multiple of the
polynomial is qc-reducible to zero in one step by one of them.
Such a property of a set of polynomials is called qc-saturation.
In example 7 the multiples
 and
and
 give us a qc-saturating set for p = a2+a.
give us a qc-saturating set for p = a2+a.
Definition 11
A set
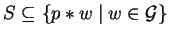
is called a
qc-saturating set for a non-zero polynomial
p in
![${\bf K}[{\cal G}]$](img5.gif)
,
if for all
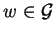
,

.
A set of polynomials
![$F \subseteq {\bf K}[{\cal G}]$](img212.gif)
is called
qc-saturated, if for all
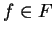
and
for all
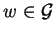
,

.
A further consequence of the previous lemmata is that finite
qc-saturating sets exist and that they can be computed.
llProcedureQUASI-COMMUTATIVE SATURATION
Given: A non-zero polynomial
![$p \in {\bf K}[{\cal G}]$](img677.gif) .
Find:
.
Find:
 ,
a qc-saturating set for p.
for all
,
a qc-saturating set for p.
for all
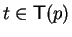 do
St :=
do
St := 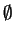 ;
if t can be brought to head position
then compute
;
if t can be brought to head position
then compute
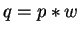 with
with
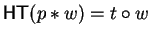 Ht :=
Ht :=
 ;
% These are candidates for ``smaller'' polynomials with t-head terms
q :=
;
% These are candidates for ``smaller'' polynomials with t-head terms
q :=
 ;
St :=
;
St := 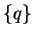 ;
endif
endfor
;
endif
endfor
 :=
:=
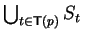 % S contains at most
% S contains at most
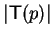 polynomials
polynomials
Notice that more structural information can be used to rule out unnecessary
candidates from the set Ht to make this procedure more efficient.
While in the free Abelian group case symmetrized sets and qc-saturation
are successfully used to repair the same deficiency such sets in general
will not coincide.
One reason is that Sims uses a different ordering on his elements.
For example a qc-saturating set for the polynomial
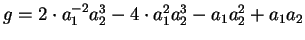 on page
on page ![[*]](http://www.mathematik.uni-kl.de/%7Ezca/icons.gif/cross_ref_motif.gif) is
is
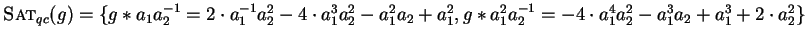 while the symmetrized set consisted of the polynomials
while the symmetrized set consisted of the polynomials
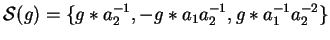 .
.
Lemma 12
For a saturated set F of polynomials in
![${\bf K}[{\cal G}]$](img5.gif) ,
,
 holds.
holds.
Proof :
1.11.1
 is an
immediate consequence of the definition of qc-reduction.
To show that the converse also holds, let
is an
immediate consequence of the definition of qc-reduction.
To show that the converse also holds, let
 .
Then
.
Then
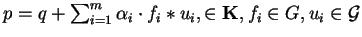 and we show that
and we show that
 by induction on m.
Without loss of generality we can assume that for every
multiple
by induction on m.
Without loss of generality we can assume that for every
multiple
 ,
,
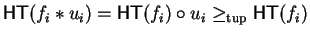 holds.
In case m=0 we are done as then p=q.
Hence let
holds.
In case m=0 we are done as then p=q.
Hence let
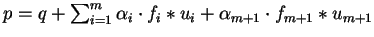 .
Then the induction hypothesis yields
.
Then the induction hypothesis yields
 .
Now let
.
Now let
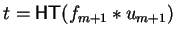 and
and
 .
Furthermore, let
.
Furthermore, let  respectively
respectively  be the coefficient of t
in q respectively
be the coefficient of t
in q respectively
 .
Then in case
.
Then in case
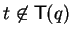 we get
we get
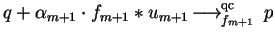 .
In case
.
In case
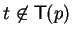 we similarly get
we similarly get
 .
As
.
As
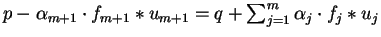 the
induction hypothesis yields
the
induction hypothesis yields
 and hence we are done.
Otherwise
let
and hence we are done.
Otherwise
let
 be the coefficient of t in
be the coefficient of t in
 and
and
 the coefficient of t in q.
the coefficient of t in q.
This gives us a qc-reduction step
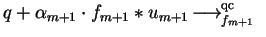
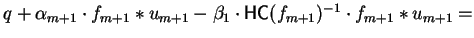
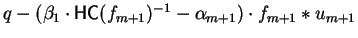
eliminating the occurrence of t in
 .
.
Then obviously
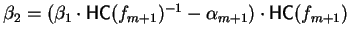 and, therefore, we have
and, therefore, we have
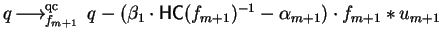 ,
i.e.,
q and
,
i.e.,
q and
 are joinable.
are joinable.
q.e.d.
1.11
Let us now proceed to characterize right Gröbner bases by so-called s-polynomials corresponding to qc-reduction.
Definition 12
For
![$p_{1}, p_{2} \!\in \!{\bf K}[{\cal G}]$](img866.gif)
such that
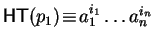
and
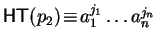
with either
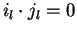
or
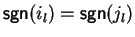
for
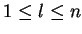
we can define an
s-polynomial, and setting
the situation
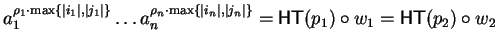
for some
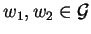
gives us
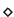
Notice that
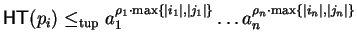 for
for
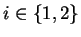 holds in case such an s-polynomial exists.
Furthermore, if there exists a term t such that
holds in case such an s-polynomial exists.
Furthermore, if there exists a term t such that
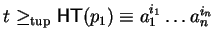 and
and
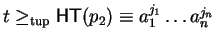 ,
an s-polynomial always exists since then the condition for the existence of an s-polynomial is fulfilled as the tuple-ordering requires that the exponent of a letter ai in the tuple-smaller term is either zero or has the same sign as the exponent of ai in the tuple-larger term.
We even have
,
an s-polynomial always exists since then the condition for the existence of an s-polynomial is fulfilled as the tuple-ordering requires that the exponent of a letter ai in the tuple-smaller term is either zero or has the same sign as the exponent of ai in the tuple-larger term.
We even have
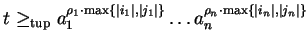 .
.
Again for the case of free Abelian groups this definition corresponds to the definition of
critical pairs for Laurent polynomials and the resulting t-polynomials are
a specialization of these s-polynomials for the integer group ring13.
We now can give a characterization of a right Gröbner basis in a familiar way using the concept of qc-saturation.
Theorem 3
For a qc-saturated set
![$G \subseteq {\bf K}[{\cal G}]$](img599.gif) the following statements are equivalent:
the following statements are equivalent:
- 1.
- For all polynomials
 we have
we have
 .
.
- 2.
- For all polynomials
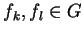 we have
we have
 .
.
Proof :
1.11.1
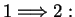 By definition 12 in case for
By definition 12 in case for
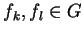 the s-polynomial exists we get
the s-polynomial exists we get

and then
 .
.
 We have to show that every non-zero element
We have to show that every non-zero element
 is
is
 -reducible to zero.
Without loss of generality we assume that G contains no constant polynomials, as then we are done at once.
Remember that for
-reducible to zero.
Without loss of generality we assume that G contains no constant polynomials, as then we are done at once.
Remember that for
 ,
,
 implies
implies
 .
Thus as
.
Thus as
 is Noetherian
it suffices to show that every
is Noetherian
it suffices to show that every
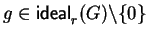 is
is
 -reducible.
Let
-reducible.
Let
 be a
representation of a non-zero polynomial g such that
be a
representation of a non-zero polynomial g such that
 .
Since G is qc-saturated we can assume
.
Since G is qc-saturated we can assume
 ,
where
,
where
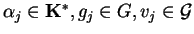 and
and
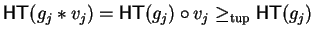 .
Depending on this representation of g and our well-founded
total ordering on
.
Depending on this representation of g and our well-founded
total ordering on  we define
we define
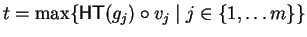 and
K is the number of polynomials
and
K is the number of polynomials
 containing t as a term.
Then
containing t as a term.
Then
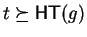 and
in case
and
in case
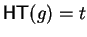 this immediately implies that g is
this immediately implies that g is
 -reducible.
Otherwise we show that
g has a special representation (a standard representation
corresponding to qc-reduction which is a right commutative prefix standard representation) where all terms are
bounded by
-reducible.
Otherwise we show that
g has a special representation (a standard representation
corresponding to qc-reduction which is a right commutative prefix standard representation) where all terms are
bounded by
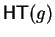 ,
as this implies that g is
top-reducible using G.
This will be done by induction on (t,K), where
(t',K')<(t,K) if and only if
,
as this implies that g is
top-reducible using G.
This will be done by induction on (t,K), where
(t',K')<(t,K) if and only if
 or
(t'=t and K'<K).
Note that this ordering is well-founded
since
or
(t'=t and K'<K).
Note that this ordering is well-founded
since
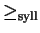 is and
is and
 .
In case
.
In case
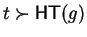 there are two (not necessarily different) polynomials gk,gl in the corresponding
representation
such that
there are two (not necessarily different) polynomials gk,gl in the corresponding
representation
such that
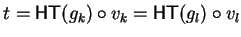 and we have
and we have
 ,
,
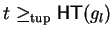 .
Hence by definition 12 there exists an s-polynomial
.
Hence by definition 12 there exists an s-polynomial




Next: 6. Reduction in Polycyclic
Up: Introducing Reduction to Polycyclic
Previous: 4. On the Relations
| ZCA Home |
Reports |
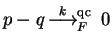 .
In the base case k=0 there is nothing to show.
Hence, let
.
In the base case k=0 there is nothing to show.
Hence, let
 .
Then by (1) there are polynomials
.
Then by (1) there are polynomials
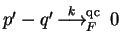 yields
the existence of a polynomial
yields
the existence of a polynomial
![]() as desired in case it
exists and that the element w need not be known for this computation.
Hence we can enrich a polynomial by the set of those multiples which bring
other terms of the polynomial to head position.
But still there remain cases of multiples which are not qc-reducible
by this set of polynomials due to the fact that the ``divisibility''
criteria for the head term does not hold.
Just take a look at the polynomial p = a2+a in our example.
Then the head term of the multiple
as desired in case it
exists and that the element w need not be known for this computation.
Hence we can enrich a polynomial by the set of those multiples which bring
other terms of the polynomial to head position.
But still there remain cases of multiples which are not qc-reducible
by this set of polynomials due to the fact that the ``divisibility''
criteria for the head term does not hold.
Just take a look at the polynomial p = a2+a in our example.
Then the head term of the multiple
![]() results from the head
term a2 of p, but still
results from the head
term a2 of p, but still
![]() is not qc-reducible by p, since
a2 is no commutative prefix of a.
Therefore, let us consider some further special multiples.
For a polynomial p and a term
is not qc-reducible by p, since
a2 is no commutative prefix of a.
Therefore, let us consider some further special multiples.
For a polynomial p and a term
![]() we call a term s
in a multiple
we call a term s
in a multiple ![]() a t-term if
a t-term if
![]() .
The following lemma states that if in two right multiples of a polynomial
the head terms result from the same term t, then there is also a
right multiple of the polynomial with a t-term as head term which is in
some sense a common commutative prefix of the head terms of the
original two multiples.
In example 7 for
.
The following lemma states that if in two right multiples of a polynomial
the head terms result from the same term t, then there is also a
right multiple of the polynomial with a t-term as head term which is in
some sense a common commutative prefix of the head terms of the
original two multiples.
In example 7 for
![]() and
and
![]() ,
both head terms result from the same term a2 and
the head term a of
,
both head terms result from the same term a2 and
the head term a of
![]() is a commutative prefix of the
head term a2 of
is a commutative prefix of the
head term a2 of
![]() .
.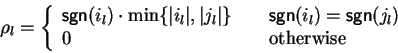
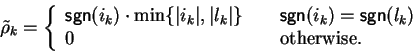
 with
with
![]() and
and
![]() give us a qc-saturating set for p = a2+a.
give us a qc-saturating set for p = a2+a.. Find:
, a qc-saturating set for p. for all
do St :=
; if t can be brought to head position then compute
with
Ht :=
; % These are candidates for ``smaller'' polynomials with t-head terms q :=
; St :=
; endif endfor
:=
% S contains at most
polynomials
![]() on page
on page ![]() is
is
![]() while the symmetrized set consisted of the polynomials
while the symmetrized set consisted of the polynomials
![]() .
.
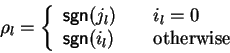
![]() We have to show that every non-zero element
We have to show that every non-zero element
![]() is
is
![]() -reducible to zero.
Without loss of generality we assume that G contains no constant polynomials, as then we are done at once.
Remember that for
-reducible to zero.
Without loss of generality we assume that G contains no constant polynomials, as then we are done at once.
Remember that for
![]() ,
,
![]() implies
implies
![]() .
Thus as
.
Thus as
![]() is Noetherian
it suffices to show that every
is Noetherian
it suffices to show that every
![]() is
is
![]() -reducible.
Let
-reducible.
Let
![]() be a
representation of a non-zero polynomial g such that
be a
representation of a non-zero polynomial g such that
![]() .
Since G is qc-saturated we can assume
.
Since G is qc-saturated we can assume
![]() ,
where
,
where
![]() and
and
![]() .
Depending on this representation of g and our well-founded
total ordering on
.
Depending on this representation of g and our well-founded
total ordering on ![]() we define
we define
![]() and
K is the number of polynomials
and
K is the number of polynomials
![]() containing t as a term.
Then
containing t as a term.
Then
![]() and
in case
and
in case
![]() this immediately implies that g is
this immediately implies that g is
![]() -reducible.
Otherwise we show that
g has a special representation (a standard representation
corresponding to qc-reduction which is a right commutative prefix standard representation) where all terms are
bounded by
-reducible.
Otherwise we show that
g has a special representation (a standard representation
corresponding to qc-reduction which is a right commutative prefix standard representation) where all terms are
bounded by
![]() ,
as this implies that g is
top-reducible using G.
This will be done by induction on (t,K), where
(t',K')<(t,K) if and only if
,
as this implies that g is
top-reducible using G.
This will be done by induction on (t,K), where
(t',K')<(t,K) if and only if
![]() or
(t'=t and K'<K).
Note that this ordering is well-founded
since
or
(t'=t and K'<K).
Note that this ordering is well-founded
since
![]() is and
is and
![]() .
In case
.
In case
![]() there are two (not necessarily different) polynomials gk,gl in the corresponding
representation
such that
there are two (not necessarily different) polynomials gk,gl in the corresponding
representation
such that
![]() and we have
and we have
![]() ,
,
![]() .
Hence by definition 12 there exists an s-polynomial
.
Hence by definition 12 there exists an s-polynomial
![]()