Next: 7. Concluding Remarks
Up: Introducing Reduction to Polycyclic
Previous: 5. Reduction in Nilpotent
6. Reduction in Polycyclic Group Rings
Let  be a polycyclic group given by a convergent PCP-presentation.
As we have seen in section 2,
due to the more general form of the commutation rules,
lemma 5
no longer holds for right multiples.
But using lemma 6 , we can define a reduction based on
commutative prefixes now using left multiples which enables us to study
left ideal congruences, and later on even ideal congruences.
be a polycyclic group given by a convergent PCP-presentation.
As we have seen in section 2,
due to the more general form of the commutation rules,
lemma 5
no longer holds for right multiples.
But using lemma 6 , we can define a reduction based on
commutative prefixes now using left multiples which enables us to study
left ideal congruences, and later on even ideal congruences.
Definition 14
Let
p,
f be two non-zero polynomials in
![${\bf K}[{\cal G}]$](img5.gif)
.
We say that
f left polycyclic (lpc-)reduces p to
q at
a monomial
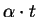
of
p in one step, denoted by
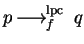
,
if
- (a)
-
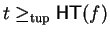 ,
and
,
and
- (b)
-
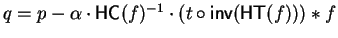 .
.
Lpc-reduction by a set
![$F \subseteq {\bf K}[{\cal G}]$](img212.gif)
is denoted by
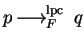
and abbreviates
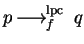
for some
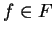
.
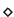
Notice that if f lpc-reduces p at
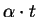 to q,
then t no longer is a term in q and by lemma 6, p > q holds.
This reduction is effective, as it is possible to decide, whether we have
to q,
then t no longer is a term in q and by lemma 6, p > q holds.
This reduction is effective, as it is possible to decide, whether we have
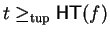 .
Further it is Noetherian and the translation lemma holds.
.
Further it is Noetherian and the translation lemma holds.
Lemma 13
Let F be a set of polynomials in
![${\bf K}[{\cal G}]$](img5.gif) and
and
![$p,q,h \in{\bf K}[{\cal G}]$](img567.gif) some
polynomials.
some
polynomials.
- 1.
- Let
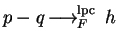 .
Then there are polynomials
.
Then there are polynomials
![$p',q' \in {\bf K}[{\cal G}]$](img569.gif) such that
such that
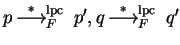 and h=p'-q'.
and h=p'-q'.
- 2.
- Let 0 be a normal form of p-q with respect to
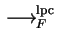 .
Then there exists a polynomial
.
Then there exists a polynomial
![$g \in {\bf K}[{\cal G}]$](img572.gif) such that
such that
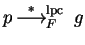 and
and
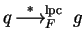 .
.
Proof :
1.11.1
This can be shown as lemma 9.
q.e.d.
1.11
Gröbner bases as defined by Buchberger can now be specified for
left ideals in this setting as before.
Definition 15
A set
![$G \subseteq {\bf K}[{\cal G}]$](img599.gif)
is said to be a
left Gröbner basis, if
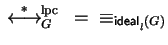
,
and
is confluent.
Again we find that in our setting we have to be more careful, as for
lpc-reduction
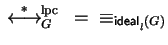 in general does not hold.
One reason for this phenomenon is that a reduction step is not preserved under
left multiplication with elements of
in general does not hold.
One reason for this phenomenon is that a reduction step is not preserved under
left multiplication with elements of  .
.
Example 9
Let
![${\bf Q}[{\cal G}]$](img602.gif)
be the group ring given in example
5.
Then similar to example
7
for the polynomials
p =
a2 +
a and
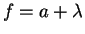
we
find that
p is lpc-reducible by
f.
This is no longer true for the multiple
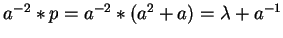
.
Notice that, since
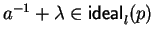
we have
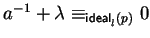
,
but
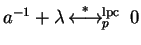
does not hold.
We will now introduce how we can extend the expressiveness of
lpc-reduction.
We start by enabling the reducibility of special monomial multiples
of a polynomial by allowing to use not only the
polynomial itself but a special set of polynomial multiples for lpc-reduction.
First let us take a look at what multiples are appropriate to later
on enable an effective characterization of a left Gröbner basis.
We proceed similar to the case of qc-reduction for nilpotent groups rings.
Lemma 14
Let p be a non-zero polynomial in
![${\bf K}[{\cal G}]$](img5.gif) .
Then it is decidable for
.
Then it is decidable for
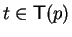 whether there exists an element
whether there exists an element
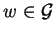 such that
such that
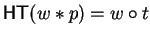 .
.
Proof :
1.11.1
We show that for a finite set of terms
 ,
where without
loss of generality t1 is the greatest term, the following holds:
In case there exists
,
where without
loss of generality t1 is the greatest term, the following holds:
In case there exists
 such that for some
such that for some
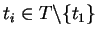 we have
we have
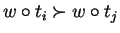 for all
for all
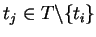 ,
then we can effectively construct
,
then we can effectively construct
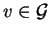 such that
such that
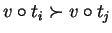 for all
for all
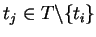 also holds without knowing w.
also holds without knowing w.
This will be done by induction on k where
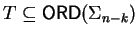 .
.
In the base case k=0 we get
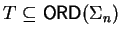 ,
hence
,
hence
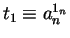 ,
,
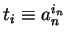 and
and
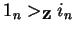 .
By our assumption there exists
.
By our assumption there exists
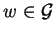 with
with
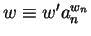 ,
,
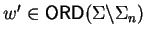 such that
such that
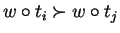 must hold for all
must hold for all
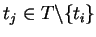 .
We have to consider two cases.
First let us assume that the letter an is not bounded.
Then let us set
.
We have to consider two cases.
First let us assume that the letter an is not bounded.
Then let us set
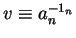 .
We have to show that for all
.
We have to show that for all
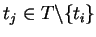 we have
we have
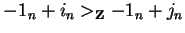 .
The case tj = t1 is trivial and for each
.
The case tj = t1 is trivial and for each
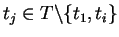 the equation is a consequence of lemma 3 as we have
the equation is a consequence of lemma 3 as we have
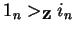 ,
,
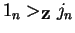 and as seen above there exists an element x, namely wn, such that
and as seen above there exists an element x, namely wn, such that
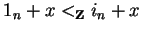 and
and
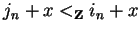 .
Now in case an is bounded by
.
Now in case an is bounded by
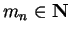 we can set
we can set
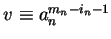 .
We find that since for all
.
We find that since for all
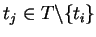 ,
we have
,
we have
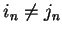 and
and
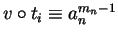 ,
for all other multiples
,
for all other multiples
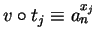 ,
xj < mn -1 must hold.
,
xj < mn -1 must hold.
In the induction step let us assume k>0 and again without loss of generality
t1 is the largest term in
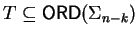 .
By our assumption there exists
.
By our assumption there exists
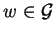 such that
such that
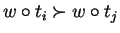 for all
for all
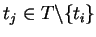 .
Let ad be the distinguishing letter between
.
Let ad be the distinguishing letter between
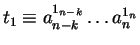 and
and
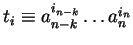 ,
and let
,
and let
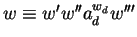 with
with
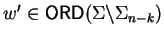 ,
,
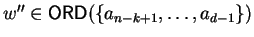 ,
,
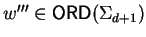 .
As before let us first consider the case that the letter ad is not bounded.
Then there exist
.
As before let us first consider the case that the letter ad is not bounded.
Then there exist
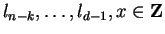 ,
,
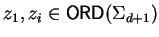 such that
such that
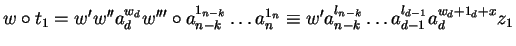 ,
,
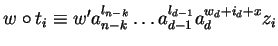 .
Now let us set
.
Now let us set
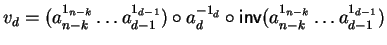 .
Since
.
Since
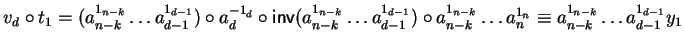 and
and
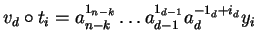 with
with
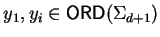 ,
,
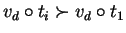 holds.
It remains to study
holds.
It remains to study
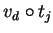 for all
for all
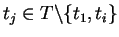 .
In case the distinguishing letter between ti and tj has index
.
In case the distinguishing letter between ti and tj has index 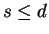 we must have
we must have
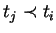 ,
as
,
as
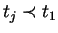 and therefore
and therefore
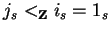 respectively
respectively
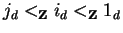 must hold.
Then
must hold.
Then
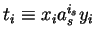 and
and
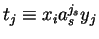 with
with
 ,
,
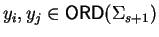 and
and
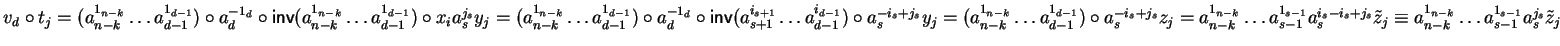 with
with
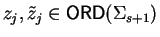 and
and similarly
and
and similarly
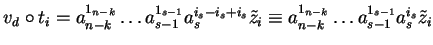 with
with
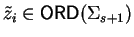 thus implying
thus implying
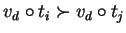 .
Otherwise let
.
Otherwise let
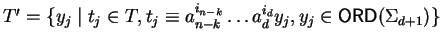 .
Then
.
Then
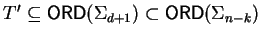 and still for
and still for
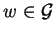 from above we can conclude
from above we can conclude
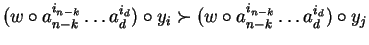 for the terms
for the terms
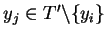 .
Hence by our induction hypothesis
.
Hence by our induction hypothesis
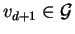 can be constructed such that
can be constructed such that
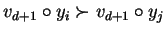 .
Now we can combine vd and vd+1 in order to construct v as follows:
let us set
.
Now we can combine vd and vd+1 in order to construct v as follows:
let us set
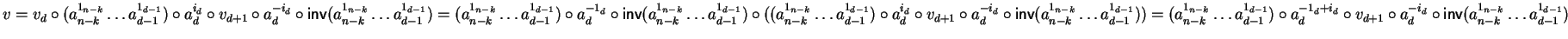 .
Then we get
.
Then we get
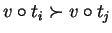 for all
for all
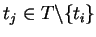 since
since
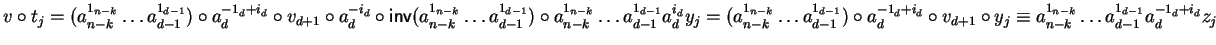 and similarly
and similarly
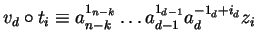 with
with
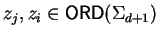 and by the definition of vd+1 we also
know
and by the definition of vd+1 we also
know
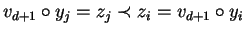 proving our claim.
proving our claim.
Now it remains to check the case where ad is bounded by md.
We can set
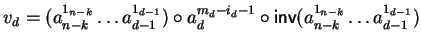 ,
and as above an element v can be constucted such that
,
and as above an element v can be constucted such that
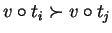 for all
for all
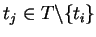 .
.
q.e.d.
1.11
Notice that the proof of this lemma shows that there is an algorithm
which computes some
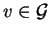 as desired in case it
exists and that the element w need not be known for this computation.
Hence we can enrich a polynomial by the set of those multiples which bring
other terms of the polynomial to head position.
But still there remain cases of multiples which are not lpc-reducible.
Just take a look at the polynomial p = a2+a in our example.
Then the head term of the multiple
as desired in case it
exists and that the element w need not be known for this computation.
Hence we can enrich a polynomial by the set of those multiples which bring
other terms of the polynomial to head position.
But still there remain cases of multiples which are not lpc-reducible.
Just take a look at the polynomial p = a2+a in our example.
Then the head term of the multiple
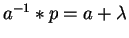 results from the head
term a2 of p, but still
results from the head
term a2 of p, but still
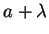 is not lpc-reducible by p,
as a2 is no commutative prefix of a.
Therefore, let us consider some further special multiples.
For a polynomial p and a term
is not lpc-reducible by p,
as a2 is no commutative prefix of a.
Therefore, let us consider some further special multiples.
For a polynomial p and a term
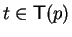 we call a term s
in a multiple
we call a term s
in a multiple 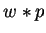 a t-term if
a t-term if
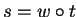 .
The following lemma states that if in two left-multiples of a polynomial
the head terms result from the same term t, then there is also a
left multiple of the polynomial with a t-term as head term which is in
some sense a common commutative prefix of the head terms of the
original two multiples.
In example 9 for
.
The following lemma states that if in two left-multiples of a polynomial
the head terms result from the same term t, then there is also a
left multiple of the polynomial with a t-term as head term which is in
some sense a common commutative prefix of the head terms of the
original two multiples.
In example 9 for
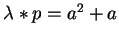 and
and
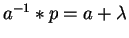 ,
both head terms result from the same term a2 and
the head term a of
,
both head terms result from the same term a2 and
the head term a of
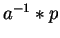 is a commutative prefix of the
head term a2 of
is a commutative prefix of the
head term a2 of
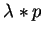 .
.
Proof :
1.11.1
Let p, 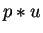 and
and 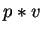 be as described in the lemma and
let the letters corresponding to our presentation be
be as described in the lemma and
let the letters corresponding to our presentation be
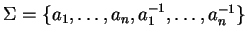 .
.
We show the existence of 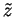 by constructing a sequence
by constructing a sequence
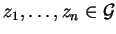 ,
such that for
,
such that for
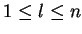 we have
we have
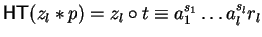 with
with
 and
and
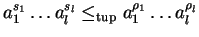 .
Then for
.
Then for
 our claim holds.
our claim holds.
Let us start by constructing an element
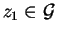 such that
such that
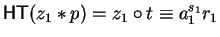 ,
,
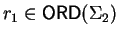 and
and
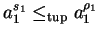 .
.
In case i1 = j1 or j1 =0 we can set z1 = v and
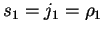 since
since
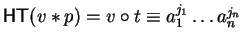 .
Similarly in case i1 = 0 we can set z1 = u and
.
Similarly in case i1 = 0 we can set z1 = u and
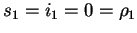 since
since
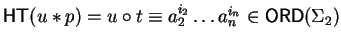 .
Hence let us assume
.
Hence let us assume
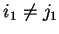 and both are non-zero.
and both are non-zero.
First suppose that
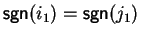 .
Notice that the proof does not depend on whether a1 is bounded or not.
Then if
.
Notice that the proof does not depend on whether a1 is bounded or not.
Then if
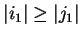 we again set z1 = v
since for
we again set z1 = v
since for
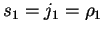 our claim holds.
In case
|j1| > |i1| we set z1 = u because for
our claim holds.
In case
|j1| > |i1| we set z1 = u because for
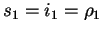 our claim holds.
our claim holds.
Now let us proceed with the case
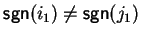 ,
hence a1 cannot be bounded.
We construct
,
hence a1 cannot be bounded.
We construct
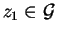 such that
such that
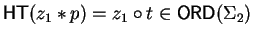 as
as
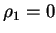 .
We claim that the letter a1 has the same exponent for all
terms in
.
We claim that the letter a1 has the same exponent for all
terms in
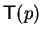 ,
say b.
In case this holds, no term in the polynomial
,
say b.
In case this holds, no term in the polynomial
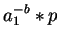 will
contain the letter a1 and the distinguishing letter between
will
contain the letter a1 and the distinguishing letter between
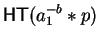 and the term
and the term
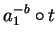 is at least of
index 2.
Furthermore we know
is at least of
index 2.
Furthermore we know
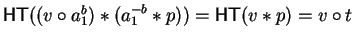 .
Thus by the construction given in the proof of
lemma 14 there exists an element
.
Thus by the construction given in the proof of
lemma 14 there exists an element
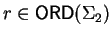 such that
such that
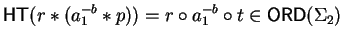 and thus we can set
and thus we can set
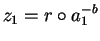 and
and
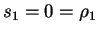 .
.
Hence it remains to prove that the exponents of a1 have the desired property.
Suppose we have the representatives
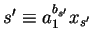 ,
,
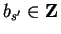 ,
,
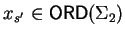 for the
terms
for the
terms
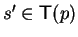 and
and
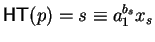 .
Then we know
.
Then we know
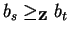 since
since
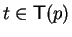 .
.
Hence in showing that the case
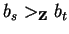 is not possible we
find that the exponents of a1 in s and t are equal.
To see this, let us study the possible cases.
If bs > 0 we have
is not possible we
find that the exponents of a1 in s and t are equal.
To see this, let us study the possible cases.
If bs > 0 we have
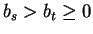 and hence there exists no
and hence there exists no
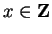 such that
such that
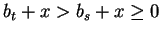 .
On the other hand bs < 0 either implies bt > 0 or
.
On the other hand bs < 0 either implies bt > 0 or
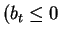 and
|bs| > |bt|).
In both cases there exists no
and
|bs| > |bt|).
In both cases there exists no
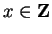 such that
bt + x < 0 and
|bt + x| > |bs + x|.
Hence bt = bs must hold as we know that t can be brought to
head position by u respectively v
such that the exponents of a1 in
such that
bt + x < 0 and
|bt + x| > |bs + x|.
Hence bt = bs must hold as we know that t can be brought to
head position by u respectively v
such that the exponents of a1 in
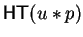 respectively
respectively
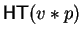 have different
sign.
have different
sign.
It remains to show that there cannot exist a term
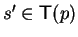 with
with
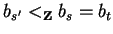 .
Let us assume such an s' exists.
Since
.
Let us assume such an s' exists.
Since
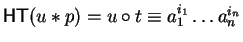 and
and
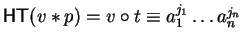 there
then must exist
there
then must exist
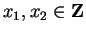 such that
such that
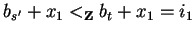 and
and
 .
Without loss of generality let us assume i1 > 0 and j1 < 0 (the
other case is symmetric).
In case bt < 0 we get that
bt + x1 = i1 > 0 implies
x1 > |bt| > 0.
Now, as
.
Without loss of generality let us assume i1 > 0 and j1 < 0 (the
other case is symmetric).
In case bt < 0 we get that
bt + x1 = i1 > 0 implies
x1 > |bt| > 0.
Now, as
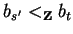 either implies
bs' > 0 or
either implies
bs' > 0 or
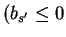 and
|bs'| < |bt|), we find
bs' + x1 > bt + x1 contradicting
and
|bs'| < |bt|), we find
bs' + x1 > bt + x1 contradicting
 .
On the other hand, in case bt > 0 we know
.
On the other hand, in case bt > 0 we know
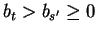 .
Furthermore,
bt + x2 = j1 < 0 implies x2 <0 and
|x2| >
bt.
Hence we get
bs' + x2 < 0 and
|bs' + x2| > |bt + x2|
contradicting
.
Furthermore,
bt + x2 = j1 < 0 implies x2 <0 and
|x2| >
bt.
Hence we get
bs' + x2 < 0 and
|bs' + x2| > |bt + x2|
contradicting
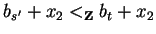 .
.
Thus let us assume that for the letter ak-1 we have
constructed
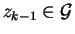 such that
such that
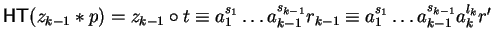 with
with
 ,
,
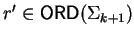 and
and
 .
We now show that we can find
.
We now show that we can find
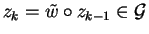 such that
such that
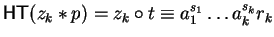 with
with
 and
and
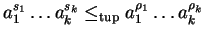 .
.
This will be done in two steps.
First we show that for the polynomials 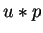 and
and
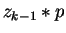 with head terms
with head terms
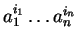 respectively
respectively
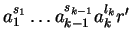 we can find an element
we can find an element
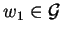 such that
such that
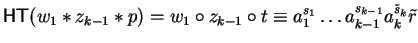 ,
,
 and
and
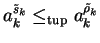 with
with
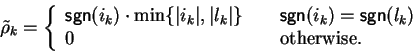
Then in case
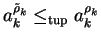 we are done
and set
we are done
and set
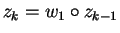 and
and
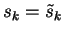 .
Else we can similarly proceed for the polynomials
.
Else we can similarly proceed for the polynomials 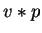 and
and
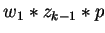 with head terms
with head terms
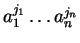 respectively
respectively
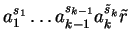 and find an element
and find an element
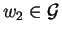 such that
for
such that
for
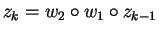 we have
we have
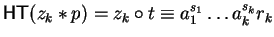 ,
,
 and
and
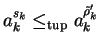 with
with
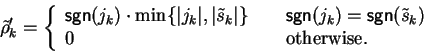
Then we can conclude
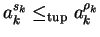 as in case sk = 0 we are immediately done and otherwise we get
as in case sk = 0 we are immediately done and otherwise we get
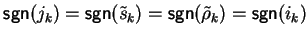 and
and
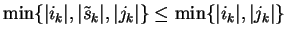 .
.
Let us hence show how to construct w1.
Remember that
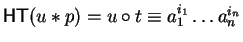 and
and
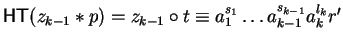 for some
for some
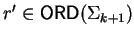 .
In case ik = lk or lk = 0 we can set
.
In case ik = lk or lk = 0 we can set
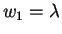 and
and
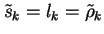 as
as
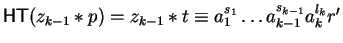 .
Hence let
.
Hence let
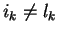 and
and
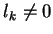 .
.
First let us assume that
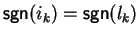 .
Without loss of generality we can assume that ak is not bounded14.
Then in case
.
Without loss of generality we can assume that ak is not bounded14.
Then in case
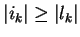 we are done by setting
we are done by setting
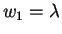 as again
as again
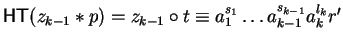 will do with
will do with
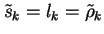 .
Therefore, let us assume that
|lk| > |ik|.
Then we consider the multiple
.
Therefore, let us assume that
|lk| > |ik|.
Then we consider the multiple
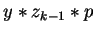 ,
where
,
where
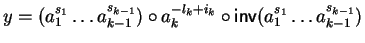 ,
i.e., the exponent of the letter ak in the term
,
i.e., the exponent of the letter ak in the term
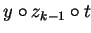 will be ik.
If
will be ik.
If
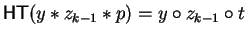 we are done because then
we are done because then
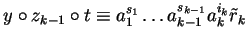 for some
for some
 and we can set w1 = y and
and we can set w1 = y and
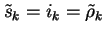 .
Otherwise we show that the t-term
.
Otherwise we show that the t-term
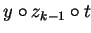 in this multiple can be brought
to head position using an element
in this multiple can be brought
to head position using an element
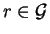 such that we have
such that we have
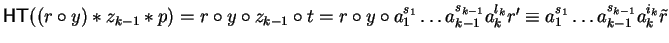 ,
where
,
where
 ,
thus allowing
to set
,
thus allowing
to set
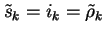 and
and
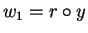 .
This follows immediately if we can prove that the exponent of ak in
the term
.
This follows immediately if we can prove that the exponent of ak in
the term
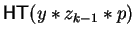 is also ik.
Then we can apply lemma 14 to the polynomial
is also ik.
Then we can apply lemma 14 to the polynomial
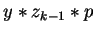 and the term
and the term
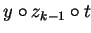 .
Note that
.
Note that
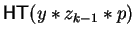 and
and
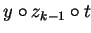 have then distinguishing letter of at least index k+1 and
further
have then distinguishing letter of at least index k+1 and
further
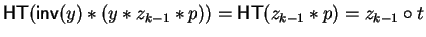 .
Therefore, we show that the exponent of ak in
the term
.
Therefore, we show that the exponent of ak in
the term
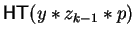 is also ik.
Let
is also ik.
Let
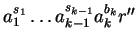 with
with
 be the term in
be the term in
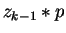 that became head
term (note that a candidate in
that became head
term (note that a candidate in
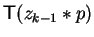 for the head term in
for the head term in
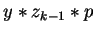 must have prefix
must have prefix
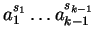 since
since
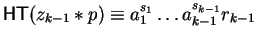 )
and multiplication with y gives us
)
and multiplication with y gives us
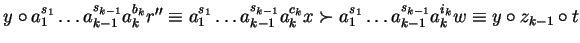 for some
for some
 and we have
and we have
 .
Then
there exist
.
Then
there exist
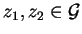 such that
such that
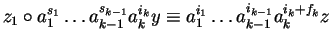 for some
for some
 and
and
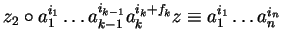 and
and
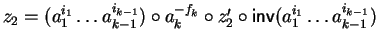 for some
for some
 .
Note that the t-term in
.
Note that the t-term in
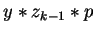 is brought to head position by
multiplication with
is brought to head position by
multiplication with
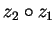 .
Now multiplying
.
Now multiplying
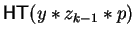 by
by
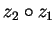 we find
we find
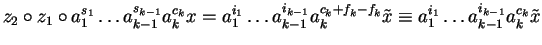 for some
for some
 .
This gives us
.
This gives us
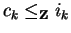 and thus
and thus
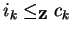 yields
ck = ik.
yields
ck = ik.
Finally, we have to check the case that
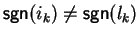 and
and
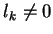 .
Notice that in this case the letter ak is not bounded.
Let us take a look at the polynomial
.
Notice that in this case the letter ak is not bounded.
Let us take a look at the polynomial
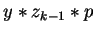 where
where
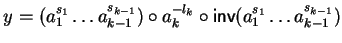 ,
i.e., the exponent of the letter ak in the term
,
i.e., the exponent of the letter ak in the term
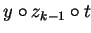 will be 0.
Suppose
will be 0.
Suppose
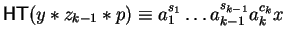 ,
for some term
,
for some term
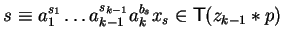 ,
,
 ,
i.e.,
ck = bs - lk.
In case this head term is already the corresponding t-term
,
i.e.,
ck = bs - lk.
In case this head term is already the corresponding t-term
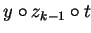 ,
we are
done and we set w1 = y and
,
we are
done and we set w1 = y and
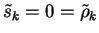 .
Now if we can show ck = 0,
by lemma 14 the t-term
.
Now if we can show ck = 0,
by lemma 14 the t-term
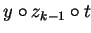 can be
brought to head position using an element as constructed in lemma 14 since
the distinguishing letter between
can be
brought to head position using an element as constructed in lemma 14 since
the distinguishing letter between
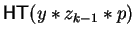 and the term
and the term
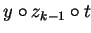 then has at least index k+1 and we know
then has at least index k+1 and we know
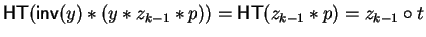 .
Hence, in showing that ck=0 we are done.
As before there exist
.
Hence, in showing that ck=0 we are done.
As before there exist
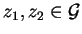 such that
such that
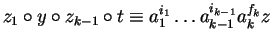 for some
for some
 and
and
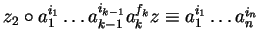 ,
i.e.,
,
i.e.,
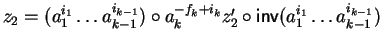 for some
for some
 .
Remember that this multiplication brings the t-term in
.
Remember that this multiplication brings the t-term in
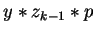 to head
position.
Hence multiplying
to head
position.
Hence multiplying
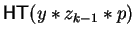 by
by
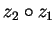 we find
we find
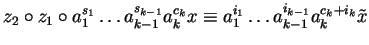 for
some
for
some
 .
Thus we know
.
Thus we know
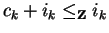 .
To see that this implies ck = 0 we have to distinguish three cases.
Remember that
ck = bs - lk and since our head term is an s-term
.
To see that this implies ck = 0 we have to distinguish three cases.
Remember that
ck = bs - lk and since our head term is an s-term 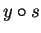 for some
for some
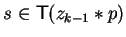 we know
we know
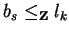 .
In case ik = 0, we have
.
In case ik = 0, we have
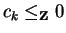 implying ck = 0.
In case ik > 0 then
implying ck = 0.
In case ik > 0 then
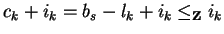 implies
implies
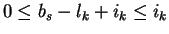 .
Furthermore, as lk < 0 we have
-lk + ik > ik implying bs < 0 and hence
.
Furthermore, as lk < 0 we have
-lk + ik > ik implying bs < 0 and hence
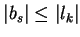 .
But then
.
But then
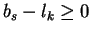 and
and
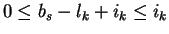 yields
ck = bs - lk = 0.
On the other hand, ik < 0 and lk > 0 imply
yields
ck = bs - lk = 0.
On the other hand, ik < 0 and lk > 0 imply
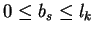 and hence
bs - lk + ik <0 yielding
and hence
bs - lk + ik <0 yielding
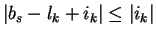 .
Since
.
Since
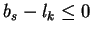 this inequation can only hold in case
ck = bs - lk = 0.
this inequation can only hold in case
ck = bs - lk = 0.
q.e.d.
1.11
These two lemmata now state that given a polynomial, we can construct
additional polynomials, which are in fact left multiples of the
original polynomial, such that every left multiple of the
polynomial is lpc-reducible to zero in one step by one of them.
Such a property of a set of polynomials is called (lpc-) saturation.
In example 9 the multiples
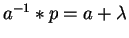 and
and
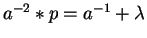 give us a lpc-saturating
set for p = a2+a.
give us a lpc-saturating
set for p = a2+a.
Definition 16
A set
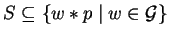
is called a
(lpc-) saturating set for a non-zero polynomial
p in
![${\bf K}[{\cal G}]$](img5.gif)
,
if for all
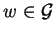
,
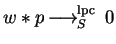
.
A set of polynomials
![$F \subseteq {\bf K}[{\cal G}]$](img212.gif)
is called
(lpc-) saturated, if for all
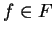
and
for all
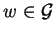
,
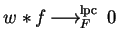
.
A further consequence of the previous lemmata is that finite
lpc-saturating sets exist and that they can be computed.
llProcedureLEFT-POLYCYCLIC SATURATION
Given: A non-zero polynomial
![$p \in {\bf K}[{\cal G}]$](img677.gif) .
Find:
.
Find:
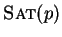 ,
a lpc-saturating set for p.
for all
,
a lpc-saturating set for p.
for all
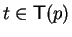 do
St :=
do
St :=  ;
if t can be brought to head position
then compute
;
if t can be brought to head position
then compute
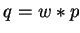 with
with
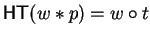 Ht :=
Ht :=
 ;
% These are candidates for ``smaller'' polynomials with t-head terms
q :=
;
% These are candidates for ``smaller'' polynomials with t-head terms
q :=
 ;
St :=
;
St := 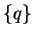 ;
endif
endfor
;
endif
endfor
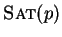 :=
:=
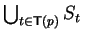 % S contains at most
% S contains at most
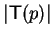 polynomials
polynomials
Notice that this is only a naive procedure and more structural information should
be used, e.g. to rule out unnecessary candidates from the sets Ht.
Lemma 16
For a lpc-saturated set F of polynomials in
![${\bf K}[{\cal G}]$](img5.gif) ,
,
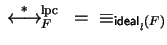 holds.
holds.
Proof :
1.11.1
This can be shown as in the proof of lemma 12.
q.e.d.
1.11
Let us now proceed to characterize left Gröbner bases by so-called s-polynomials corresponding to lpc-reduction.
Definition 17
For
![$p_{1}, p_{2} \!\in \!{\bf K}[{\cal G}]$](img866.gif)
such that
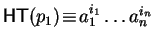
and
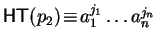
with either
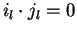
or
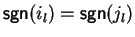
for
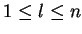
we can define an
s-polynomial, and setting
the situation
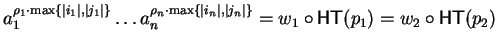
for some
w1,
w2 in

gives us
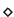
Notice that
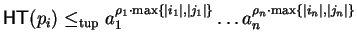 for
for
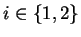 holds in case such an s-polynomial exists.
Furthermore, if there exists a term t such that
holds in case such an s-polynomial exists.
Furthermore, if there exists a term t such that
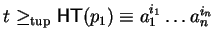 and
and
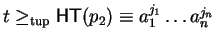 ,
an s-polynomial always exists since then the condition for its existence is fulfilled as the tuple ordering requires that the exponent of a letter ai in the tuple-smaller term is either zero or has the same sign as the exponent of ai in the tuple-larger term.
We even have
,
an s-polynomial always exists since then the condition for its existence is fulfilled as the tuple ordering requires that the exponent of a letter ai in the tuple-smaller term is either zero or has the same sign as the exponent of ai in the tuple-larger term.
We even have
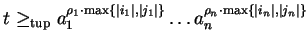 .
.
We now can give a characterization of a left Gröbner basis in a familiar way using the concept of lpc-saturation.
Theorem 7
For a lpc-saturated set
![$G \subseteq {\bf K}[{\cal G}]$](img599.gif) the following statements are equivalent:
the following statements are equivalent:
- 1.
- For all polynomials
 we have
we have
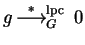 .
.
- 2.
- For all polynomials
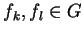 we have
we have
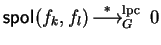 .
.
Proof :
1.11.1
Again we can follow the lines of the proof given for the similar
theorem 3 for nilpotent groups and qc-reduction.
q.e.d.
1.11
It is also possible to give a characterization of left Gröbner bases in terms of standard representations.
Corollary 3
For a set
![$G \subseteq {\bf K}[{\cal G}]$](img599.gif) the following statements are equivalent:
the following statements are equivalent:
- 1.
- For all polynomials
 we have
we have
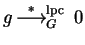 .
.
- 2.
- Every
 has a left commutative prefix standard representation.
has a left commutative prefix standard representation.
- 3.
- G is a left commutative prefix standard basis.
- 4.
- G is a left Gröbner basis.
Now, using the characterization given in theorem 7
we can state a procedure which
enumerates left Gröbner bases in polycyclic group rings.
ProcedureLEFT GR¨OBNER BASES IN POLYCYCLIC GROUP RINGS
Given: A finite set of polynomials
![$F \subseteq {\bf K}[{\cal G}]$](img212.gif) .
Find:
.
Find:
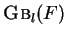 ,
a left Gröbner basis of
,
a left Gröbner basis of
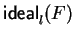 .
G :=
.
G :=
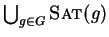 ;% G is lpc-saturated and
;% G is lpc-saturated and
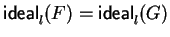 B :=
B :=
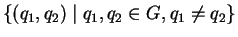 ;
while
;
while
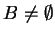 do % Test if statement 2 of theorem 7 is valid
(q1, q2) :=
do % Test if statement 2 of theorem 7 is valid
(q1, q2) :=
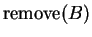 ;% Remove an element using a fair strategy
if h :=
;% Remove an element using a fair strategy
if h :=
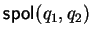 exists
then h' :=
exists
then h' :=
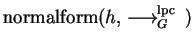 ;
% Compute a normal form
if
;
% Compute a normal form
if 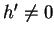 % The s-polynomial does not reduce to zero
then G :=
% The s-polynomial does not reduce to zero
then G :=
 ;% G is lpc-saturated and
;% G is lpc-saturated and
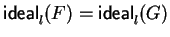 B :=
B :=
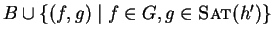 ;
endif
endif
endwhile
;
endif
endif
endwhile
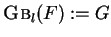
The set G enumerated by this naive procedure fulfills the requirements of
theorem 7, i.e., the set G at each stage generates
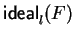 and is lpc-saturated.
Using a fair strategy to remove elements from the test set B ensures
that for all polynomials entered into G the s-polynomials are considered
in case they exist.
Hence, in case the procedure terminates, it computes a left Gröbner basis.
The next theorem states that every left Gröbner basis contains a finite one and hence this procedure must terminate.
and is lpc-saturated.
Using a fair strategy to remove elements from the test set B ensures
that for all polynomials entered into G the s-polynomials are considered
in case they exist.
Hence, in case the procedure terminates, it computes a left Gröbner basis.
The next theorem states that every left Gröbner basis contains a finite one and hence this procedure must terminate.
Theorem 8
Every left Gröbner basis contains a finite one.
Proof :
1.11.1
Since lpc-reduction is based on commutative prefixes this can
be shown using Dickson's lemma as in the proof of theorem
5.
q.e.d.
1.11
Let us now continue to show how again Gröbner bases of two-sided
ideals can be characterized by left Gröbner bases which have
additional properties.
We will call a set of polynomials a Gröbner basis of the
two-sided ideal it generates, if it fulfills one of the equivalent
statements in the next theorem.
Theorem 9
For a set of polynomials
![$G \subseteq {\bf K}[{\cal G}]$](img599.gif) , assuming that
, assuming that  is
presented by
is
presented by
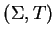 as described above, the following properties
are equivalent:
as described above, the following properties
are equivalent:
- 1.
- G is a left Gröbner basis and
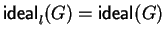 .
.
- 2.
- For all
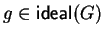 we have
we have
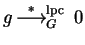 .
.
- 3.
- G is a left Gröbner basis and for all
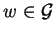 ,
,
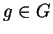 we have
we have
 .
.
- 4.
- G is a left Gröbner basis and for all
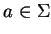 ,
,
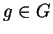 we have
we have
 .
.
Proof :
1.11.1
This can be shown as in the proof of theorem 4.
q.e.d.
1.11
Statement 4 enables a constructive approach to use procedure LEFT GR¨OBNER BASES IN POLYCYCLIC GROUP RINGS in order to compute
Gröbner bases of two-sided ideals and item 2 states that such bases
can be used to decide the membership problem for the two-sided ideal
by using lpc-reduction.
The following corollary similar to theorem 7
can be used as the foundation
of a procedure to compute two-sided Gröbner bases.
Corollary 4
For a lpc-saturated set
![$G \subseteq {\bf K}[{\cal G}]$](img599.gif) the following statements are equivalent:
the following statements are equivalent:
- 1.
- For all polynomials
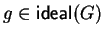 we have
we have
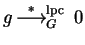 .
.
- 2.
- (a)
- For all polynomials
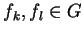 we have
we have
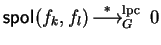 .
.
- (b)
- For all
 ,
,
 we have
we have
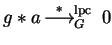 .
.
Again the existence of finite Gröbner bases is a consequence of Dickson's Lemma.
Notice that so far we only have characterized lpc-saturated Gröbner bases.
Of course there also exist Gröbner bases which are not lpc-saturated.
It is even possible to introduce interreduction for lpc-reduction
and to compute
reduced Gröbner bases which are unique in case
we demand that the polynomials are monic, i.e., they have head coeffient 1.
Definition 18
We call a set of polynomials
![$F \subseteq {\bf K}[{\cal G}]$](img212.gif) interreduced
interreduced or
reduced with respect to
,
if no polynomial
f in
F is lpc-reducible by the other polynomials in
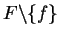
.
Theorem 10
Every (left) ideal in
![${\bf K}[{\cal G}]$](img5.gif) contains
a unique monic finite reduced (left) Gröbner basis.
contains
a unique monic finite reduced (left) Gröbner basis.
Proof :
1.11.1
The proof again can be done using standard techniques as in the case of
ordinary polynomial rings.
q.e.d.
1.11
Such reduced Gröbner bases can be computed by incorporating interreduction
into the respective procedures.
Let us close this section by sketching a possible approach to
treat right ideals in polycyclic group rings.
As seen in section 2 a stability property for right
multiples need not hold when using the idea of commutative prefixes for
reduction if  is given by a convergent PCP-presentation.
Furthermore, Wißmann's result given in section 4
for the existence of only
is given by a convergent PCP-presentation.
Furthermore, Wißmann's result given in section 4
for the existence of only 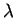 -confluent bases in case
the group is given by a convergent PCP-system, states that in general
no finite Gröbner bases will exist when using weakenings of strong
reduction and every reduction based on commutative prefixes and using
right multiples is such a weakening.
Anyhow, a similar approach is possible in case we change the presentation of
our polycyclic group.
Let
-confluent bases in case
the group is given by a convergent PCP-system, states that in general
no finite Gröbner bases will exist when using weakenings of strong
reduction and every reduction based on commutative prefixes and using
right multiples is such a weakening.
Anyhow, a similar approach is possible in case we change the presentation of
our polycyclic group.
Let
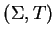 be a convergent PCP-presentation of a polycyclic
group.
Then the presentation
be a convergent PCP-presentation of a polycyclic
group.
Then the presentation
 ,
where
,
where
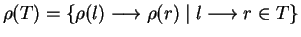 and
and
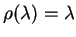 ,
,
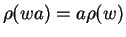 ,
is again a polycyclic power presentation which is convergent15
with respect to the syllable ordering now with status right, i.e.,
the syllables are compared from the right to the left.
Such a presentation will be called a reversed polycyclic power
commutation presentation (with status right).
The irreducible elements now are reversed ordered words of the form
,
is again a polycyclic power presentation which is convergent15
with respect to the syllable ordering now with status right, i.e.,
the syllables are compared from the right to the left.
Such a presentation will be called a reversed polycyclic power
commutation presentation (with status right).
The irreducible elements now are reversed ordered words of the form
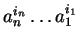 ,
i.e.,
,
i.e.,
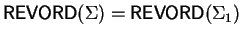 ,
where we define
,
where we define
 recursively by
recursively by
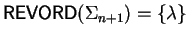 ,
and
,
and
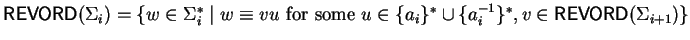 .
We can show similar
properties as in the case of Wißmann's PCP-presentations.
.
We can show similar
properties as in the case of Wißmann's PCP-presentations.
Lemma 17
Let  be a polycyclic group with
be a polycyclic group with
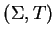 a convergent reversed polycyclic
power commutation presentation with
status right.
Further for some
a convergent reversed polycyclic
power commutation presentation with
status right.
Further for some
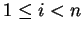 let
let
 .
Then we have
.
Then we have
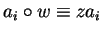 for some
for some
 .
.
Based on the form of the rules occurring in the presentation
of  we can again prove stability for certain right multiples.
From now on we will always assume that
we can again prove stability for certain right multiples.
From now on we will always assume that  is presented by
a convergent reversed polycyclic power commutation system
with status right.
is presented by
a convergent reversed polycyclic power commutation system
with status right.
Lemma 18
Let  be a group presented by a convergent reversed
polycyclic power commutation system
with status right and
be a group presented by a convergent reversed
polycyclic power commutation system
with status right and
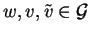 with
with
 and
and
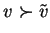 .
Then for
.
Then for
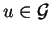 such that
such that
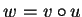 , we get
, we get
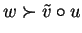 .
Notice that since
.
Notice that since  is a group, u always exists and is unique,
namely
is a group, u always exists and is unique,
namely
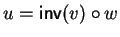 .
.
The proof of this lemma and the ones follwing in the remaining part
of this section follow the lines of the proofs given for the
comparable facts for lpc-reduction due to the symmetrical situation
provided by the form of the reversed presentation of  .
We now proceed to study an appropriate reduction based on
commutative prefixes for this setting.
.
We now proceed to study an appropriate reduction based on
commutative prefixes for this setting.
Definition 19
Let
p,
f be two non-zero polynomials in
![${\bf K}[{\cal G}]$](img5.gif)
.
We say that
f right polycyclic (rpc-) reduces p to
q at
a monomial
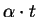
of
p in one step, denoted by
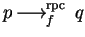
,
if
- (a)
-
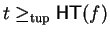 ,
and
,
and
- (b)
-
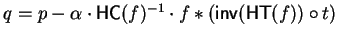 .
.
Rpc-reduction by a set
![$F \subseteq {\bf K}[{\cal G}]$](img212.gif)
is denoted by
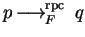
and abbreviates
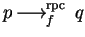
for some
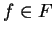
.
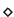
Notice that if f rpc-reduces p at
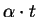 to q,
then t no longer is a term in q and by lemma 18, p > q holds.
This reduction is effective, as it is possible to decide, whether we have
to q,
then t no longer is a term in q and by lemma 18, p > q holds.
This reduction is effective, as it is possible to decide, whether we have
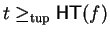 .
Further it is Noetherian and the translation lemma holds.
.
Further it is Noetherian and the translation lemma holds.
Lemma 19
Let F be a set of polynomials in
![${\bf K}[{\cal G}]$](img5.gif) and
and
![$p,q,h \in{\bf K}[{\cal G}]$](img567.gif) some
polynomials.
some
polynomials.
- 1.
- Let
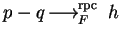 .
Then there are
.
Then there are
![$p',q' \in {\bf K}[{\cal G}]$](img569.gif) such that
such that
 and h=p'-q'.
and h=p'-q'.
- 2.
- Let 0 be a normal form of p-q with respect to
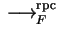 .
Then there exists a polynomial
.
Then there exists a polynomial
![$g \in {\bf K}[{\cal G}]$](img572.gif) such that
such that
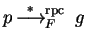 and
and
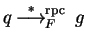 .
.
Gröbner bases as defined by Buchberger can now be specified for
right ideals in this setting as follows.
Definition 20
A set
![$G \subseteq {\bf K}[{\cal G}]$](img599.gif)
is said to be a
Gröbner basis with respect to rpc-reduction, if
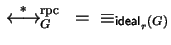
,
and
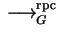
is confluent.
As before, in general we do not have the property
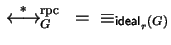 ,
but it can be restored by saturation due to the following lemmata:
,
but it can be restored by saturation due to the following lemmata:
Lemma 20
Let p be a non-zero polynomial in
![${\bf K}[{\cal G}]$](img5.gif) .
Then it is decidable whether for
.
Then it is decidable whether for
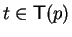 there exists an element
there exists an element
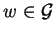 such that
such that
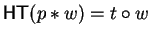 .
.
Definition 21
A set
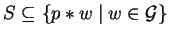
is called an
(rpc-) saturating set for a non-zero polynomial
p in
![${\bf K}[{\cal G}]$](img5.gif)
,
if for all
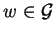
,
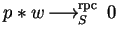
.
A set of polynomials
![$F \subseteq {\bf K}[{\cal G}]$](img212.gif)
is called
(rpc-) saturated, if for all
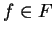
and
for all
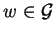
,
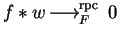
.
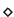
Lemma 22
For a rpc-saturated set F of polynomials in
![${\bf K}[{\cal G}]$](img5.gif) ,
,
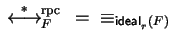 holds.
holds.
Now it remains to give a confluence criteria which can be done
using s-polynomials a usual.
Definition 22
For
![$p_{1}, p_{2} \!\in \!{\bf K}[{\cal G}]$](img866.gif)
such that
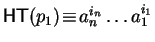
and
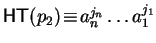
with either
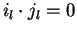
or
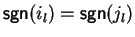
for
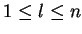
,
we can define an
s-polynomial, and setting
the situation
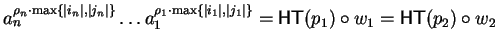
for some
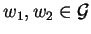
gives us
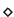
Theorem 11
For a saturated set
![$G \subseteq {\bf K}[{\cal G}]$](img599.gif) the following statements are equivalent:
the following statements are equivalent:
- 1.
- For all polynomials
 we have
we have
 .
.
- 2.
- For all polynomials
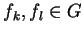 we have
we have
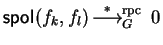 .
.
Procedures to compute rpc-saturating sets and Gröbner bases with
respect to rpc-reduction can be given as in the case of lpc-reduction
before.
Again the concept of interreduction can be supplied to yield
unique monic reduced Gröbner bases, and it is
possible to characterize two-sided ideals by right ideals using
the same ideas as cited before.
Let us close this section by showing how in fact reversed polycyclic
power commutation presentations
and rpc-reduction yield a solution to the subgroup problem in polycylic
groups giving rise to confluent bases of the subgroup.
Example 10
Let

be the group specified on page
![[*]](http://www.mathematik.uni-kl.de/%7Ezca/icons.gif/cross_ref_motif.gif)
now presented
by a convergent
reversed polycyclic power commutation presentation
assuming a syllable ordering with precedence
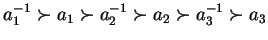
and status right,
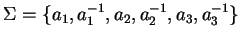
,
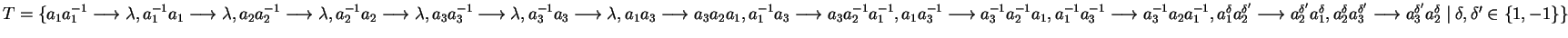
.
Then for the right ideal generated by
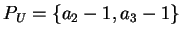
the set
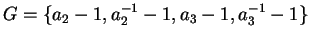
is a Gröbner basis
corresponding to the subgroup generated by
U.
While in the setting of example
4 the elements
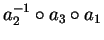
and
a1 have no common descendant with respect
to
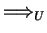
,
now we find that the normal form
a3a2-1a1 of the element
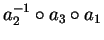
is reducible by
G as follows:
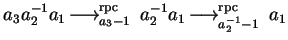
.
Hence now
a3a2-1a1 and
a1 are clearly joinable.



Next: 7. Concluding Remarks
Up: Introducing Reduction to Polycyclic
Previous: 5. Reduction in Nilpotent
| ZCA Home |
Reports |
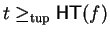 ,
and
,
and
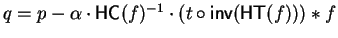 .
.
![]() as desired in case it
exists and that the element w need not be known for this computation.
Hence we can enrich a polynomial by the set of those multiples which bring
other terms of the polynomial to head position.
But still there remain cases of multiples which are not lpc-reducible.
Just take a look at the polynomial p = a2+a in our example.
Then the head term of the multiple
as desired in case it
exists and that the element w need not be known for this computation.
Hence we can enrich a polynomial by the set of those multiples which bring
other terms of the polynomial to head position.
But still there remain cases of multiples which are not lpc-reducible.
Just take a look at the polynomial p = a2+a in our example.
Then the head term of the multiple
![]() results from the head
term a2 of p, but still
results from the head
term a2 of p, but still
![]() is not lpc-reducible by p,
as a2 is no commutative prefix of a.
Therefore, let us consider some further special multiples.
For a polynomial p and a term
is not lpc-reducible by p,
as a2 is no commutative prefix of a.
Therefore, let us consider some further special multiples.
For a polynomial p and a term
![]() we call a term s
in a multiple
we call a term s
in a multiple ![]() a t-term if
a t-term if
![]() .
The following lemma states that if in two left-multiples of a polynomial
the head terms result from the same term t, then there is also a
left multiple of the polynomial with a t-term as head term which is in
some sense a common commutative prefix of the head terms of the
original two multiples.
In example 9 for
.
The following lemma states that if in two left-multiples of a polynomial
the head terms result from the same term t, then there is also a
left multiple of the polynomial with a t-term as head term which is in
some sense a common commutative prefix of the head terms of the
original two multiples.
In example 9 for
![]() and
and
![]() ,
both head terms result from the same term a2 and
the head term a of
,
both head terms result from the same term a2 and
the head term a of
![]() is a commutative prefix of the
head term a2 of
is a commutative prefix of the
head term a2 of
![]() .
.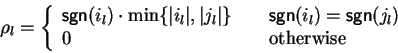
![]() by constructing a sequence
by constructing a sequence
![]() ,
such that for
,
such that for
![]() we have
we have
![]() with
with
![]() and
and
![]() .
Then for
.
Then for
![]() our claim holds.
our claim holds.
![]() such that
such that
![]() ,
,
![]() and
and
![]() .
.
![]() since
since
![]() .
Similarly in case i1 = 0 we can set z1 = u and
.
Similarly in case i1 = 0 we can set z1 = u and
![]() since
since
![]() .
Hence let us assume
.
Hence let us assume
![]() and both are non-zero.
and both are non-zero.
![]() .
Notice that the proof does not depend on whether a1 is bounded or not.
Then if
.
Notice that the proof does not depend on whether a1 is bounded or not.
Then if
![]() we again set z1 = v
since for
we again set z1 = v
since for
![]() our claim holds.
In case
|j1| > |i1| we set z1 = u because for
our claim holds.
In case
|j1| > |i1| we set z1 = u because for
![]() our claim holds.
our claim holds.
![]() ,
hence a1 cannot be bounded.
We construct
,
hence a1 cannot be bounded.
We construct
![]() such that
such that
![]() as
as
![]() .
We claim that the letter a1 has the same exponent for all
terms in
.
We claim that the letter a1 has the same exponent for all
terms in
![]() ,
say b.
In case this holds, no term in the polynomial
,
say b.
In case this holds, no term in the polynomial
![]() will
contain the letter a1 and the distinguishing letter between
will
contain the letter a1 and the distinguishing letter between
![]() and the term
and the term
![]() is at least of
index 2.
Furthermore we know
is at least of
index 2.
Furthermore we know
![]() .
Thus by the construction given in the proof of
lemma 14 there exists an element
.
Thus by the construction given in the proof of
lemma 14 there exists an element
![]() such that
such that
![]() and thus we can set
and thus we can set
![]() and
and
![]() .
.
![]() ,
,
![]() ,
,
![]() for the
terms
for the
terms
![]() and
and
![]() .
Then we know
.
Then we know
![]() since
since
![]() .
.
![]() is not possible we
find that the exponents of a1 in s and t are equal.
To see this, let us study the possible cases.
If bs > 0 we have
is not possible we
find that the exponents of a1 in s and t are equal.
To see this, let us study the possible cases.
If bs > 0 we have
![]() and hence there exists no
and hence there exists no
![]() such that
such that
![]() .
On the other hand bs < 0 either implies bt > 0 or
.
On the other hand bs < 0 either implies bt > 0 or
![]() and
|bs| > |bt|).
In both cases there exists no
and
|bs| > |bt|).
In both cases there exists no
![]() such that
bt + x < 0 and
|bt + x| > |bs + x|.
Hence bt = bs must hold as we know that t can be brought to
head position by u respectively v
such that the exponents of a1 in
such that
bt + x < 0 and
|bt + x| > |bs + x|.
Hence bt = bs must hold as we know that t can be brought to
head position by u respectively v
such that the exponents of a1 in
![]() respectively
respectively
![]() have different
sign.
have different
sign.
![]() with
with
![]() .
Let us assume such an s' exists.
Since
.
Let us assume such an s' exists.
Since
![]() and
and
![]() there
then must exist
there
then must exist
![]() such that
such that
![]() and
and
![]() .
Without loss of generality let us assume i1 > 0 and j1 < 0 (the
other case is symmetric).
In case bt < 0 we get that
bt + x1 = i1 > 0 implies
x1 > |bt| > 0.
Now, as
.
Without loss of generality let us assume i1 > 0 and j1 < 0 (the
other case is symmetric).
In case bt < 0 we get that
bt + x1 = i1 > 0 implies
x1 > |bt| > 0.
Now, as
![]() either implies
bs' > 0 or
either implies
bs' > 0 or
![]() and
|bs'| < |bt|), we find
bs' + x1 > bt + x1 contradicting
and
|bs'| < |bt|), we find
bs' + x1 > bt + x1 contradicting
![]() .
On the other hand, in case bt > 0 we know
.
On the other hand, in case bt > 0 we know
![]() .
Furthermore,
bt + x2 = j1 < 0 implies x2 <0 and
|x2| >
bt.
Hence we get
bs' + x2 < 0 and
|bs' + x2| > |bt + x2|
contradicting
.
Furthermore,
bt + x2 = j1 < 0 implies x2 <0 and
|x2| >
bt.
Hence we get
bs' + x2 < 0 and
|bs' + x2| > |bt + x2|
contradicting
![]() .
.
![]() such that
such that
![]() with
with
![]() ,
,
![]() and
and
![]() .
We now show that we can find
.
We now show that we can find
![]() such that
such that
![]() with
with
![]() and
and
![]() .
.
![]() and
and
![]() with head terms
with head terms
![]() respectively
respectively
![]() we can find an element
we can find an element
![]() such that
such that
![]() ,
,
![]() and
and
![]() with
with
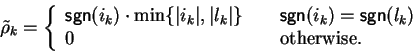
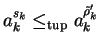 with
with
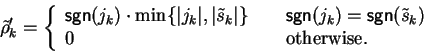
![]() and
and
![]() give us a lpc-saturating
set for p = a2+a.
give us a lpc-saturating
set for p = a2+a.. Find:
, a lpc-saturating set for p. for all
do St :=
; if t can be brought to head position then compute
with
Ht :=
; % These are candidates for ``smaller'' polynomials with t-head terms q :=
; St :=
; endif endfor
:=
% S contains at most
polynomials
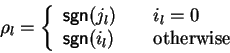
. Find:
, a left Gröbner basis of
. G :=
;% G is lpc-saturated and
B :=
; while
do % Test if statement 2 of theorem 7 is valid (q1, q2) :=
;% Remove an element using a fair strategy if h :=
exists then h' :=
; % Compute a normal form if
% The s-polynomial does not reduce to zero then G :=
;% G is lpc-saturated and
B :=
; endif endif endwhile
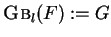
![]() and is lpc-saturated.
Using a fair strategy to remove elements from the test set B ensures
that for all polynomials entered into G the s-polynomials are considered
in case they exist.
Hence, in case the procedure terminates, it computes a left Gröbner basis.
The next theorem states that every left Gröbner basis contains a finite one and hence this procedure must terminate.
and is lpc-saturated.
Using a fair strategy to remove elements from the test set B ensures
that for all polynomials entered into G the s-polynomials are considered
in case they exist.
Hence, in case the procedure terminates, it computes a left Gröbner basis.
The next theorem states that every left Gröbner basis contains a finite one and hence this procedure must terminate.![]() is given by a convergent PCP-presentation.
Furthermore, Wißmann's result given in section 4
for the existence of only
is given by a convergent PCP-presentation.
Furthermore, Wißmann's result given in section 4
for the existence of only ![]() -confluent bases in case
the group is given by a convergent PCP-system, states that in general
no finite Gröbner bases will exist when using weakenings of strong
reduction and every reduction based on commutative prefixes and using
right multiples is such a weakening.
Anyhow, a similar approach is possible in case we change the presentation of
our polycyclic group.
Let
-confluent bases in case
the group is given by a convergent PCP-system, states that in general
no finite Gröbner bases will exist when using weakenings of strong
reduction and every reduction based on commutative prefixes and using
right multiples is such a weakening.
Anyhow, a similar approach is possible in case we change the presentation of
our polycyclic group.
Let
![]() be a convergent PCP-presentation of a polycyclic
group.
Then the presentation
be a convergent PCP-presentation of a polycyclic
group.
Then the presentation
![]() ,
where
,
where
![]() and
and
![]() ,
,
![]() ,
is again a polycyclic power presentation which is convergent15
with respect to the syllable ordering now with status right, i.e.,
the syllables are compared from the right to the left.
Such a presentation will be called a reversed polycyclic power
commutation presentation (with status right).
The irreducible elements now are reversed ordered words of the form
,
is again a polycyclic power presentation which is convergent15
with respect to the syllable ordering now with status right, i.e.,
the syllables are compared from the right to the left.
Such a presentation will be called a reversed polycyclic power
commutation presentation (with status right).
The irreducible elements now are reversed ordered words of the form
![]() ,
i.e.,
,
i.e.,
![]() ,
where we define
,
where we define
![]() recursively by
recursively by
![]() ,
and
,
and
![]() .
We can show similar
properties as in the case of Wißmann's PCP-presentations.
.
We can show similar
properties as in the case of Wißmann's PCP-presentations.