


Next: Bibliography
Up: Introducing Reduction to Polycyclic
Previous: 6. Reduction in Polycyclic
In this paper we have shown how Gröbner basis methods can be
successfully introduced to nilpotent respectively polycyclic
group rings.
We have illustrated how depending on the respective group presentations
commutative divisors can be used to define Noetherian reductions.
Left ideals can be handled by so called lpc-reduction using
convergent PCNI- as well as PCP-systems for presenting the group.
For right ideals we have to be more careful.
While the collecting process induced by convergent PCNI-presentations
allows to define a Noetherian reduction using right multiples,
this cannot be generalized for convergent PCP-systems.
Hence we have introduced reversed PCP-systems with status right
and in this setting again reduction can be specified.
The results can be summarized as follws:
| Group presentation |
left GBs |
right GBs |
two-sided GBs |
|---|
| PCNI-system |
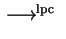 |
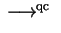 |
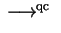 |
| |
|
|
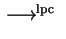 |
| PCP-system |
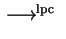 |
none16 |
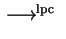 |
| reversed PCP-system |
none |
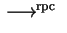 |
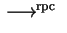 |
In [Re95] we have shown how the theory of Gröbner bases in
monoid and group rings over fields can be lifted to monoid and group
rings over reduction rings fulfilling special axioms, e.g., allowing
to compute finite Gröbner bases for ideals in the coefficient
domain.
Hence the results of this paper also hold for nilpotent respectively polycyclic group rings
over reduction rings, e.g., the integers  .
.
Finally we want to sketch how the results of this report can be lifted
to group rings over nilpotent-by-finite respectively polycyclic-by-finite
groups.
Essential in this approach is the use of semi-Thue systems related to
extensions of groups as introduced for context-free groups by Cremanns and
Otto in [CrOt94].
Details of the lifting process for respective group rings can be found in
[Re95] and [MaRe96].
The key idea is to combine a convergent presentation
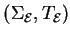 of a finite group
of a finite group 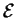 with a convergent PCNI-presentation
respecitively PCP-presentation of a nilpotent respectively polycyclic
group
with a convergent PCNI-presentation
respecitively PCP-presentation of a nilpotent respectively polycyclic
group 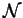 presented by
presented by
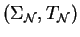 .
Assuming
.
Assuming
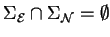 ,
let
,
let
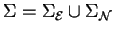 and let T consist of the set of rules
and let T consist of the set of rules
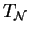 ,
and
the following additional rules:
,
and
the following additional rules:
l
 rwr for all
rwr for all
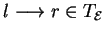 ,
where
,
where
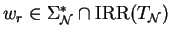 ,
xa
,
xa
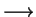 awx for all
awx for all
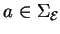 ,
for all
,
for all
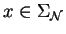 ,
where
,
where
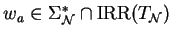 .
.
Then in case
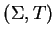 is convergent it
is called the extension presentation of
is convergent it
is called the extension presentation of  as an extension of
as an extension of 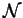 by
by 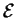 (see e.g. [Cr95]).
Every element in
(see e.g. [Cr95]).
Every element in  has a representative of the form eu where
has a representative of the form eu where
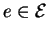 and
and
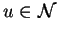 .
We can specify a total well-founded ordering
.
We can specify a total well-founded ordering  on our group
by combining a
total well-founded ordering
on our group
by combining a
total well-founded ordering
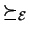 on
on 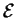 and
the syllable ordering
and
the syllable ordering
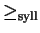 on
on 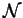 :
For
:
For
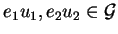 we define
we define
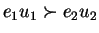 if and
only if
if and
only if
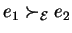 or
(e1 = e2 and
or
(e1 = e2 and
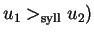 .
Furthermore, we can lift the tuple ordering to
.
Furthermore, we can lift the tuple ordering to  as follows:
For two elements eu, ev, we define
as follows:
For two elements eu, ev, we define
 if
if
 and
we define
and
we define
 .
According to this ordering we call ev a (commutative)
prefix of eu if
.
According to this ordering we call ev a (commutative)
prefix of eu if
 and
introducing the concept of
and
introducing the concept of 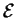 -closure as in [Re95] or
[MaRe96] we can proceed to prove lemmata and theorems similar to
those in section 5 and 6.
-closure as in [Re95] or
[MaRe96] we can proceed to prove lemmata and theorems similar to
those in section 5 and 6.



Next: Bibliography
Up: Introducing Reduction to Polycyclic
Previous: 6. Reduction in Polycyclic
| ZCA Home |
Reports |
![]() of a finite group
of a finite group ![]() with a convergent PCNI-presentation
respecitively PCP-presentation of a nilpotent respectively polycyclic
group
with a convergent PCNI-presentation
respecitively PCP-presentation of a nilpotent respectively polycyclic
group ![]() presented by
presented by
![]() .
Assuming
.
Assuming
![]() ,
let
,
let
![]() and let T consist of the set of rules
and let T consist of the set of rules
![]() ,
and
the following additional rules:
,
and
the following additional rules:
rwr for all
, where
, xa
awx for all
, for all
, where
.