INPUT: Q - a representation matrix of the module, k - an integer.
OUTPUT: L=A,B,C,D - a list of matrices presenting the blocks of a good
presentation matrix (B is a zero matrix).
First prepare the input matrix Q according to (5.2):
![]()
INPUT: Q - a representation matrix of the module, k - an integer.
OUTPUT: L=A,B,C,D - a list of matrices presenting the blocks of a good
presentation matrix (B is a zero matrix).
The next procedure computes generators of the module of J-row reductions of Q:
![]()
INPUT: L=A,B,C,D - a list of matrices.
OUTPUT:
![]() - a list of constant
matrices corresponding to generators of
- a list of constant
matrices corresponding to generators of
![]() .
.
Here ko_hom computes the matrix of the map defined by inserting the matrix in the first place of the Hom-functor and kontra_hom does the same with the second argument.
Next we will test J-row-minimality and possibly find a row-reduction
of Q:
![]()
INPUT: L=A,B,C,D - a list of block matrices of Q,
![]() - a list of constant matrices
- a list of constant matrices
OUTPUT: Q - a presentation matrix,
bool= FALSE if Q was J-row-minimal,
break= FALSE if there is no unique J-row-minimal.
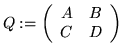
In the main loop a J-row-minimal presentation matrix is iterated or
we obtain the answer, according to Proposition 13, that there is no J-row-splitting
of the module.
![]()
INPUT: as above
OUTPUT: Q - a matrix being J-row-minimal if bool = TRUE
or Q does not have a unique J-row-minimal presenatation matrix otherwise.
If break = TRUE, a final test, which uses Corollary 8,
must be preformed to determine whether
the presentation matrix allows a J-splitting. Otherwise we shall take the
next subset J.
![]()
INPUT: as above
OUTPUT: Q0 - a block diagonal presentation matrix if bool =
TRUE
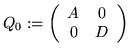
Remarks: