Let
In this chapter we shall prove that Schreyer's method to compute syzygies
(cf. [S1], [S2], [E]) extends to any semigroup ordering < on
![]() .
For the treatment of syzygies in a different
context, or for different algorithms see [M2], [Ba], [MM],
[MMT] and
[LS].
.
For the treatment of syzygies in a different
context, or for different algorithms see [M2], [Ba], [MM],
[MMT] and
[LS].
Let
![]() be a standard basis of
be a standard basis of
![]() .
.
For
![]() we choose the following
Schreyer ordering <1 (depending on S):
we choose the following
Schreyer ordering <1 (depending on S):
![]() if and only
if either
if and only
if either
![]() or
or
![]() and i > j.
and i > j.
For gi, gj having the leading term in the same component, that is
![]() we consider spoly
(gi, gj)
:= mjigi - mijgj with
we consider spoly
(gi, gj)
:= mjigi - mijgj with
![]() .
.
Because S is a standard basis we obtain (Corollary 1.11)
For j > i such that gi, gj have leading term in the same component, let
Let ker
![]() denote
the module of syzygies, syz(I), of
denote
the module of syzygies, syz(I), of
![]() .
The
following proposition is essentially due to Schreyer.
.
The
following proposition is essentially due to Schreyer.
Proof: 1)
![]() holds by definition of <1.
holds by definition of <1.
To prove 2) it has to be shown that
![]() (Definition 1.3).
(Definition 1.3).
Let
![]() ,
that is
,
that is
![]() syz(I), and
let
syz(I), and
let
![]() with respect to <1. Let
with respect to <1. Let
But
![]() implies
implies
![]() ,
that is
,
that is
![]() ,
which proves
the proposition.
,
which proves
the proposition.
The principle of the algorithm is now easy.
Let S be a standard basis of
![]() .
We may assume that
.
We may assume that
![]() L(s') for different
L(s') for different
![]() .
.
Let ![]() .
.
W := Syz![]()
INPUT: S, a standard basis
OUTPUT: W, the module of syzygies of S
T := initSyz![]()
INPUT: S, a standard basis
![]()
OUTPUT: T, the set
![]()
h := NF(s|T)
INPUT: S, a polynomial vector to reduce
T, a set of polynomials with which to reduce
OUTPUT: h, the reduced ponyomial vector
Here we use on
![]() the following
ordering <2:
the following
ordering <2:
If ![]() and
and
![]() then
m ej <2 n ei for all
monomials
then
m ej <2 n ei for all
monomials
![]() .
.
On
![]() respectively
respectively
![]() we use
the extension of < (respectively <1) described in Chapter 1.
we use
the extension of < (respectively <1) described in Chapter 1.
The algorithm is extremely sensitive with respect to the ordering of the standard basis S of the input.
Assuming that the set L is ordered as in Chapter 1, then S should be ordered in an opposite manner to Chapter 1, that is it should be ordered by decreasing monomial ordering. This produces potentially more syzygies of smaller degree at the beginning.
Because of Proposition 4.1 we know the leading term of the
s-polynomial of a pair in L without conputing the s-polynomial. If
this leading term is divisible by another one, the pair can be cancelled from
L.
The algorithm ``Standard basis'' of paragraph 1, together with repeated application of the algorithm ``Syz'', provides an effective way to construct finite Loc;SPMlt; K[x]-free resolutions and gives a sharpened version of Hilbert's syzygy theorem which generalizes Schreyer's proof (cf. [E], [S1], [S2]).
Let
![]() be a standard basis of
be a standard basis of
![]() .
We assume that the leading terms
are a basis vector of K[x]r, that is
.
We assume that the leading terms
are a basis vector of K[x]r, that is
![]() .
We set
.
We set
![]() s.t.
s.t.
![]() and for
and for ![]() we
choose exactly one
we
choose exactly one ![]() such that
such that
![]() .
Then ILoc;SPMlt;
K[x] is a free Loc;SPMlt; K[x]-module with basis
.
Then ILoc;SPMlt;
K[x] is a free Loc;SPMlt; K[x]-module with basis
![]() and
(Loc
;SPMlt; K[x])r/ILoc;SPMlt;K[x] is Loc;SPMlt; K[x]-free with basis represented
by the
and
(Loc
;SPMlt; K[x])r/ILoc;SPMlt;K[x] is Loc;SPMlt; K[x]-free with basis represented
by the
![]() .
.
Proof: Let us renumber the gi such that
![]() for
for ![]() .
First of all, the subset
.
First of all, the subset
![]() remains a standard basis of I since the set of
leading terms is not changed. Hence, we may assume that all leading terms are
different.
By Proposition 1.4,
remains a standard basis of I since the set of
leading terms is not changed. Hence, we may assume that all leading terms are
different.
By Proposition 1.4,
![]() generates ILoc;SPMlt; K[x]. Now consider a relation
generates ILoc;SPMlt; K[x]. Now consider a relation
After clearing denominators we may assume that
![]() .
Since the
leading terms involve different ei on each side, we obtain
.
Since the
leading terms involve different ei on each side, we obtain
![]() .
This shows that the
.
This shows that the
![]() are linear
independent and that the
are linear
independent and that the
![]() are independent modulo ILoc;SPMlt;
K[x].
Since
are independent modulo ILoc;SPMlt;
K[x].
Since
![]() generate
L(K[x]r)=(e1,...,er)K[x]
generate
L(K[x]r)=(e1,...,er)K[x]
![]() is a standard basis of K[x]r this set generates
is a standard basis of K[x]r this set generates
![]() by Corollary 1.11. Therefore,
by Corollary 1.11. Therefore,
![]() generates
generates
![]() over Loc;SPMlt; K[x].
over Loc;SPMlt; K[x].
Proof: For i < j and
![]() ,
,
![]() we have
we have
![]() with
with
![]() .
Therefore,
.
Therefore,
![]() does not depend on
does not depend on
![]() .
.
Let q1 := q and
![]() the morphism given by
the morphism given by
![]() ,
,
![]() ,
and
,
and
![]() the analog morphism given by the standard basis
the analog morphism given by the standard basis
![]() ,
,
![]() .
Applying the same construction as
above to syz
.
Applying the same construction as
above to syz
![]() and
and
![]() we obtain a standard basis
we obtain a standard basis
![]() of szy2(I) := syz(syz(I)) =
ker
of szy2(I) := syz(syz(I)) =
ker
![]() such that the leading terms of
such that the leading terms of
![]() do not depend on
do not depend on
![]() .
.
Continuing in the same way we obtain an exact sequence
Moreover, ker
![]() syzn-s(I) has a standard basis
syzn-s(I) has a standard basis
![]() such that none of the variables appear in
such that none of the variables appear in
![]() .
Hence, by the preceding lemma,
.
Hence, by the preceding lemma,
![]() becomes free after tensoring with
Loc;SPMlt;K[x]. If we tensor the whole sequence with Loc;SPMlt;K[x] it stays exact
(since Loc;SPMlt;K[x] is K[x]-flat) and is the desired free resolution of M.
becomes free after tensoring with
Loc;SPMlt;K[x]. If we tensor the whole sequence with Loc;SPMlt;K[x] it stays exact
(since Loc;SPMlt;K[x] is K[x]-flat) and is the desired free resolution of M.
Example 4.5
ab+14766ac-12713bc+8997ad+1878ae,
ac+9210bc+9399ad+13903bd-9583ae,
bc-13988ad-4712bd+6771ae-7341be,
ad-2340bd-7515cd+1575ae-4211be,
bd+5023cd-874ae+4773be+14016ce,
cd+1617ae-14718be-1384ce+12060de,
a3-10731b3+5818ae2+13936be2+11725ce2+6401de2,
b3-4862c3-2334ae2+9991be2+14579ce2+10173de2,
c3-6087d3+1135ae2+4570be2+5250ce2+1393de2,
d3+11392ae2+7125be2-15188ce2-12706de2-10957e3;
(
a, b, c, d, e the order of the variables)
ab-2302ac+1504bc-2175ad-13468bd-8487ae+2984be,
ac+7021bd-2524ad-8459bd+4807cd-4372ae-1908be,
bc-1768ad+12994bd+7816cd-7083ae+2769be-354ce,
ad+8219bd-13765cd+14989ae+36be-4732ce+8648de,
a3-7986a2e-744b2e+2389c2e-7991bde+11075cde-15425d2e+7645ae2-1871be2+869
8ce2-9609de2,
a2e+3582b2e-6012c2e-14933bde+14203cde+11560d2e+2294ae2+12826be2-12284ce^
2+10870de2,
b2e+3097c2e+10611bde+6826cde+2785d2e-14231ae2+13731be2-1863ce2+8227de2,
c2e-8559bde+13444cde+3372d2e+5235ae2+9139be2-7685ce2+3756de2,
bde-14077cde-2960d2e-4481ae2-3950be2-850ce2-14832de2,
cde-13603d2e+4327ae2+15554be2+2054ce2-12484de2,
b3+7339d2e-3253ae2+8720be2+9224ce2-11849de2,
c3-9222d2e-12818ae2-11519be2+6703ce2-10364de2,
d3+4730d2e+7627ae2+14168be2+11428ce2+8632de2,
d2e+9376ae2+6688be2-11914ce2-295de2-5576e3;
(a,b,c,d,e the order of the variables)
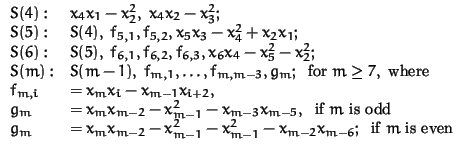
(
![]() the order of the variables)
the order of the variables)
For these examples we computed a minimal resolution with MACAULAY and SINGULAR using the regularity bound (cf. [E]) with the ordering degrevlex (in both systems realized as scripts; without this bound the computation is, at least for complicated examples, usually much slower) and computed a resolution with Schreyer's method (SING/SCHREYER).
vars denotes the number of variables, minbase the number of a minimal system
of generators, stdbase the number of elements in the standard base and dim the
dimension of the zero-set of the ideal.
For versions and notations cf. Chapter 3.
| SING | |||||||
| [-1.5ex]MAC | [-1.5ex]SING | SCHREYER | [-1.5ex]vars | [-1.5ex]dim | [-1.5ex]minbase | [-1.5ex]stdbase | |
| 1. | 552 | 96 | 13769 | 5 | 3 | 3 | 63 |
| 2. | 2222 | 87 | 6293 | 5 | 3 | 3 | 82 |
| 3. | 16 | 5 | 9 | 4 | 1 | 3 | 75 |
| 4. | 20 | 5 | 7 | 4 | 1 | 3 | 44 |
| 5. | 10 | 2 | 9 | 4 | 2 | 3 | 83 |
| 6. | 12 | 2 | 23 | 5 | 2 | 3 | 22 |
| 7. | 4 | 12 | 542 | 5 | 4 | 15 | 138 |
| 8. | 14 | 1 | 1 | 5 | 4 | 3 | 38 |
| 9. | 238 | 91 | 1228 | 5 | 1 | 5 | 76 |
| 10. | 299 | 322 | 15 | 6 | 1 | 5 | 38 |
| 11. | 950 | 166 | 2412 | 5 | 0 | 5 | 142 |
| 12. | 49 | 24 | 3 | 6 | 0 | 15 | 22 |
| 13. | 44 | 23 | 31 | 5 | 2 | 3 | 25 |
| 14. | 101 | 60 | 1 | 5 | 0 | 10 | 19 |
| 15. | 78 | 23 | 2 | 5 | 0 | 14 | 23 |
| 16. | 1 | 1 | 12 | 5 | 2 | 4 | 23 |
| 17. | 2 | 4 | 3 | 9 | 2 | 27 | 27 |
| 18. | 20 | 29 | 22 | 10 | 2 | 35 | 35 |
| 19. | 12 | 7 | 6 | 4 | 0 | 6 | 31 |
| 20. | 825 | 446 | 7958 | 4 | 0 | 6 | 192 |